怎么理解python決策樹的基本原理

本篇文章給大家分享的是有關怎么理解python決策樹的基本原理，小編覺得挺實用的，因此分享給大家學習，希望大家閱讀完這篇文章后可以有所收獲，話不多說，跟著小編一起來看看吧。

決策樹是一種非參數的監督學習方法，它主要用于分類和回歸問題。

決策樹模型通過一系列if then決策規則的集合，將特征空間劃分成有限個不相交的子區域，對于落在相同子區域的樣本，決策樹模型給出相同的預測值。

這些if then決策規則之間的層次關系形成一個樹形結構，稱之為決策樹，這些不相交的子區域和樹結構的葉子節點一一對應。

一，決策樹原理概述

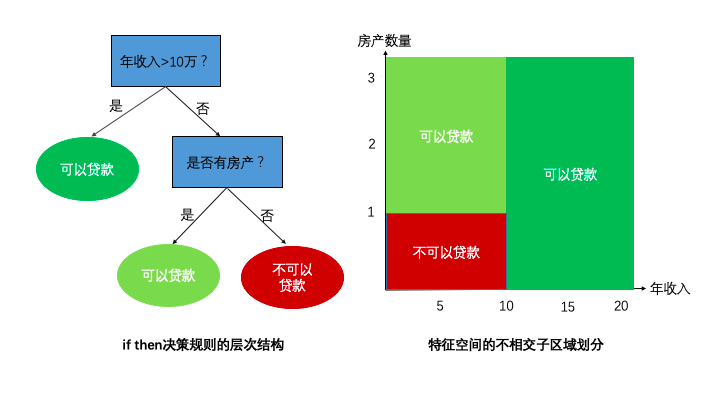
1，假設空間

下面從假設空間，目標函數，優化算法3方面闡述決策樹算法的基本原理。

假設空間即我們對模型形式的先驗假設，最終我們求得的模型必定符合我們對模型形式的先驗假設。

決策樹模型的先驗形式可以表述成如下：

其中q[x]是從特征空間映射到節點編號空間的函數。決策樹模型的關鍵是將特征空間劃分成不相交的子區域，落在相同子區域的樣本具有相同的預測值。

為了確定一棵決策樹的完備結構，要明確如下兩個方面：一是如何劃分子區域，二是子區域的預測值取多少。

2，目標函數

目標函數即我們用什么標準來評價一個模型的好壞。目標函數決定了我們從假設空間中選擇模型的偏好。

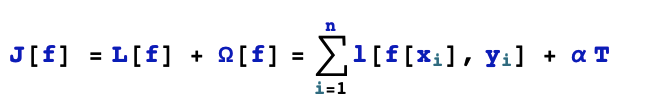
決策樹的目標函數可以用來評價一棵決策樹的好壞。這個目標函數應當包括兩個方面的內容。第一個是反應決策樹對樣本數據點擬合準確度的損失項，第二個是反應決策樹模型復雜程度的正則化項。

正則化項可以取模型的葉子節點的數量。即決策樹模型劃分得到的不相交子區域越多，我們認為模型越復雜。

對于損失項，如果是回歸問題，損失項可以取平方損失，如果是分類問題，我們可以用不純度來作為衡量標準。

為什么用不純度呢？由于決策樹的同一葉子節點上的所有樣本都取相同的預測值，如果這些樣本的真實 label 只有一種取值，那么這個葉子節點上的樣本是非常“純凈”的，我們可以直接指定預測值為這個葉子節點上 label 的取值，預測誤差為0。反之，如果葉子節點上不同樣本的 label 的取值很雜亂，所謂眾口難調，那么無論我們如何指定葉子節點上的預測值，總會有較大的預測誤差。

那么，如何來衡量不純度呢？一般有3種方法，信息熵，基尼不純度，以及分類誤差率。分類誤差率即以 label 取值最多的那個類別作為葉子節點預測值時的誤差率。信息熵和基尼不純度我們稍后介紹。

3，優化算法

優化算法指的是通過什么樣的方式調整我們的模型結構或模型超參數取值，使得模型的目標函數取值不斷降低。

優化算法決定了我們用什么樣的步驟在假設空間中尋找合適的模型。

對于決策樹而言，優化算法包括樹的生成策略和樹的剪枝策略。

樹的生成策略一般采用貪心的思想不斷選擇特征對特征空間進行切分。

樹的剪枝策略一般分為預剪枝和后剪枝策略。一般來說后剪枝策略生成的決策樹效果較好，但其計算成本也更高。

二，ID3，C4.5，CART決策樹的對比

1，適用問題范圍的不同

ID3算法只能處理離散特征的分類問題，C4.5能夠處理離散特征和連續特征的分類問題，CART算法可以處理離散和連續特征的分類與回歸問題。

2，假設空間的不同

ID3和C4.5算法使用的決策樹可以是多分叉的，而CART算法的決策樹必須是二叉樹。

3，目標函數的不同

同樣是處理分類問題時，在決定選擇哪個特征進行決策樹的分裂時，3個模型使用不同的判斷標準。ID3算法以信息增益作為標準，C4.5算法以信息增益率作為標準，而CART算法以基尼不純度增益作為標準。

4，優化算法的不同

3種算法有不同的剪枝策略。

ID3算法實際上沒有剪枝策略，當葉子節點上的樣本都屬于同一個類別或者所有特征都使用過了的情況下決策樹停止生長。

C4.5算法使用預剪枝策略，當分裂后的增益小于給定閾值或者葉子上的樣本數量小于某個閾值或者葉子節點數量達到限定值或者樹的深度達到限定值，決策樹停止生長。

CART決策樹主要使用后剪枝策略。

5，效果上的差異

ID3決策樹是最早出現的決策樹，C4.5是在它基礎上的改進，CART決策樹是更晚出現的，效果上一般而言CART樹會好于C4.5，C4.5會好于ID3.

三，熵，條件熵，信息增益，信息增益率

1，熵

熵是對某個離散隨機變量不確定性大小的一種度量。既然是反應不確定性的，我們的先驗知識是當隨機變量只有一種取值時，熵為0，當隨機變量的取值可能性越多，在各個可能性之間的概率分布越平均，熵越大。熵的計算公式滿足這些先驗的特性。注意，熵只能度量離散隨機變量的不確定性。

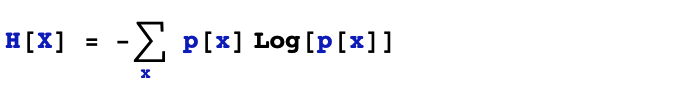
在決策樹的應用場景中，我們實際上是用經驗熵來衡量標簽取值分布的“純度”的，即用頻率分布代替概率分布進行計算。

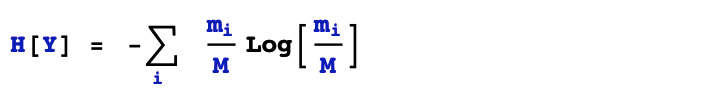
2，條件熵

所謂條件熵，是指給定隨機變量X的取值的前提下，隨機事件Y的不確定性的一種度量。

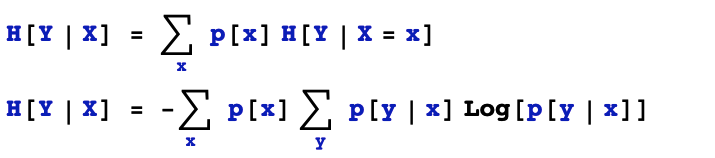
在決策樹的應用場景中，條件熵的含義更加清晰明了，即按照離散特征X的取值將樣本空間劃分成多個葉子節點，各個葉子節點上樣本標簽Y取值的熵不純度的加權平均。

3，信息增益

隨機變量X對于隨機變量Y的信息增益被定義成Y的熵和Y對X的條件熵之差。

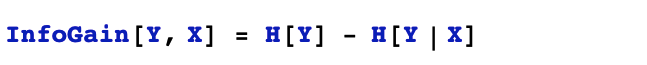
在決策樹的應用場景中，信息增益的含義就是特征X對樣本標簽Y不確定性減少的貢獻。

信息增益也叫做互信息。互信息存在如下特性，Y對X的互信息和X對Y的互信息是相等的。互信息是衡量兩個離散隨機變量之前相關性的一種常用指標。

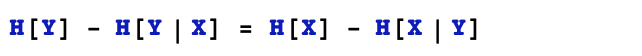
簡單證明如下：

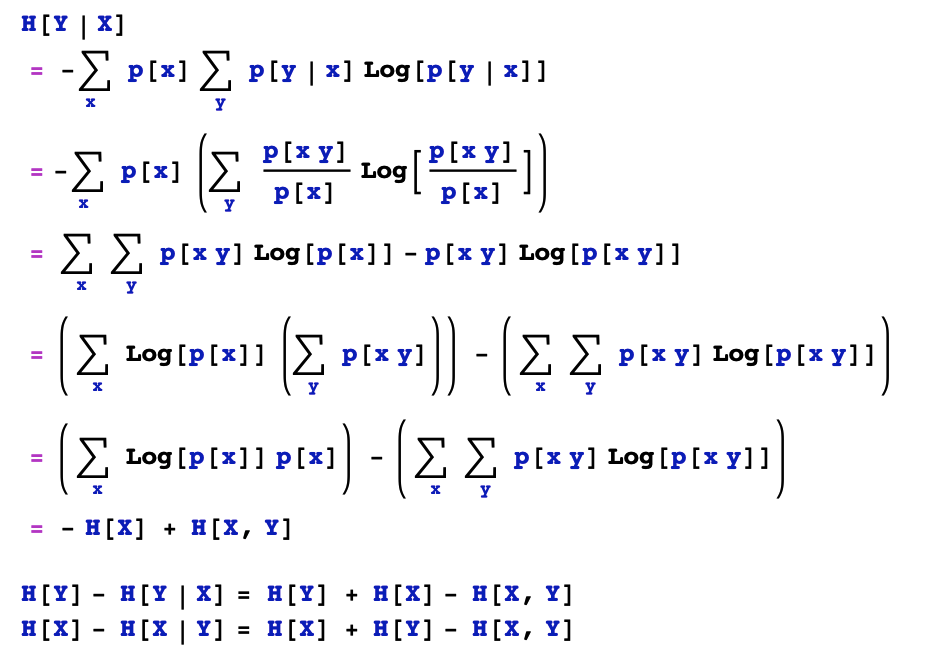
4，信息增益率

ID3模型采用信息增益作為待分裂特征的選擇標準，但是信息增益傾向于選擇特征取值數量較多的特征。C4.5用信息增益率作為待分裂特征的選擇標準，可以避免這種傾向。值得注意的是，C4.5在選擇連續特征的分裂點位的時候，依然使用信息增益作為選擇標準。

X對Y的信息增益率是X對Y的信息增益和X的熵的比值。

四，基尼不純度和基尼不純度增益

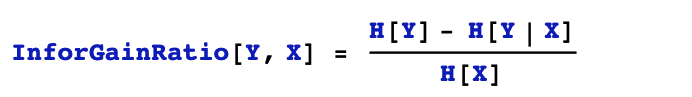
1，基尼不純度

基尼不純度和熵具有相似的作用，可以衡量一個隨機變量取值的不確定性或者說"不純凈"程度。它滿足我們的先驗預期，當隨機變量只有一種可能取值的時候，基尼不純度為0，當隨機變量的可能取值數量越多，取值概率分布越平均，基尼不純度越大。

基尼不純度的定義如下。

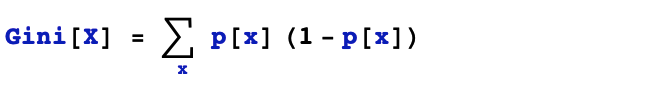
基尼不純度滿足我們對不確定性衡量指標的先驗假設。事實上，基尼不純度和熵有非常密切的關系，把熵的對數部分泰勒展開到1階，即得到基尼不純度的定義公式。

2，基尼不純度增益

基尼不純度增益和信息增益的作用非常類似。計算方法也非常相似。

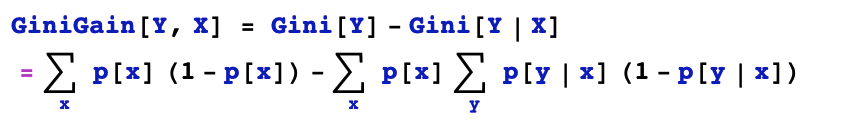
值得注意的是CART決策樹是二叉樹，在計算離散特征的基尼不純度增益時會嘗試根據特征是否取某個特定的類別把特征空間分成兩部分，而在計算連續特征的基尼不純度增益時會嘗試選擇一個分裂點位把特征空間分成兩部分。

以上就是怎么理解python決策樹的基本原理，小編相信有部分知識點可能是我們日常工作會見到或用到的。希望你能通過這篇文章學到更多知識。更多詳情敬請關注億速云行業資訊頻道。