您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
R語言中基于Logistic銀行貸款拖欠率用戶分析是怎樣的,相信很多沒有經驗的人對此束手無策,為此本文總結了問題出現的原因和解決方法,通過這篇文章希望你能解決這個問題。
今天推一篇廣義線性回歸模型中的一種,logistic回歸,去年參加校創項目,我們組的課題是’基于logistic滴滴打車女性出行安全研究‘,所以,對于這個模型,有一些了解,logistic回歸多用于醫學統計,因變量為定性變量,可以為有序、分等級的,比如有病、無病;滿意、一般、不滿意等。logistic回歸多用于尋找危險因素,比如某一疾病的危險因素有哪些?預測某病發生的概率有多大?判別某人有多大可能性是屬于某病。
建模之前,首先要有一定的數據支持。
截取部分數據如下
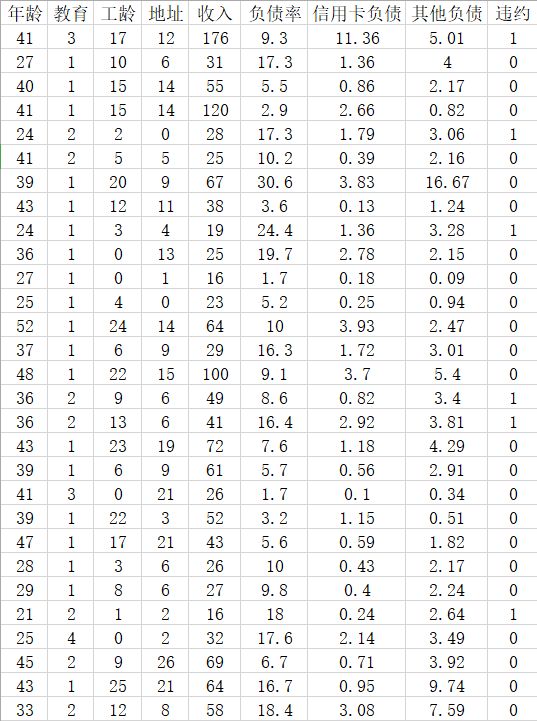

Logistic 回歸屬于概率型非線性回歸,分為二分類和多分類的回歸模型。對于二分類的Logistic回歸,因變量y只有“是、否”兩個取值,記為1和0。假設在自變量x1,x2,...,xP,作用下,y取“是”的概率是p,則取“否”的概率是1-p,研究的是當y取“是”發生的概率p與自變量x1,x2,...,xP的關系。
當自變量之間出現多重共線性時,用最小二乘估計估計的回歸系數將會不準確,消除多重共線性的參數改進的估計方法主要有嶺回歸和主成分回歸。
3.建模準備
Logistic 回歸模型的建模步驟
1)根據分析目的設置指標變量(因變量和自變量),然后收集數據。
2)y取1的概率是p=P(y=1|x),取0概率是1-p。用Ln(p/1-p)和自變量列出線性回歸方程,估計出模型中的回歸系數。
3)進行模型檢驗:根據輸出的方差分析表中的F值和p值來檢驗該回歸方程是否顯著,如果p值小于顯著性水平a則模型通過檢驗,可以進行下一步回歸系數的檢驗;否則要重新選擇指標變量,重新建立回歸方程。
4)進行回歸系數的顯著性檢驗:在多元線性回歸中,回歸方程顯著并不意味著每個自變量對y的影響都顯著,為了從回歸方程中剔除那些次要的、可有可無的變量,重新建立更為簡單有效的回歸方程,需要對每個自變量進行顯著性檢驗,檢驗結果由參數估計表得到。采用逐步回歸法,首先剔除掉最不顯著的因變量,重新構造回歸方程,一直到模型和參與的回歸系數都通過檢驗。
5)模型應用:輸入自變量的取值,就可以得到預測變量的值,或者根據預測變量的值去控制自變量的取值。

logistic回歸模型程序
# 讀入數據
Data<-read.csv("C:/Users/27342/Desktop/bankloan.csv")[2:701, ]
# 數據命名
colnames(Data)<- c("x1", "x2", "x3", "x4", "x5", "x6", "x7", "x8", "y")
# logistic回歸模型
glm <- glm(y ~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8,
family = binomial(link = logit), data = Data)
summary(glm)
# 逐步尋優法
logit.step <- step(glm, direction = "both")
summary(logit.step)
# 前向選擇法
logit.step <- step(glm, direction = "forward")
summary(logit.step)
# 后向選擇法
logit.step <- step(glm, direction = "backward")
summary(logit.step)
部分結果展示
Call:
glm(formula = y ~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8, family = binomial(link = logit),data = Data)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.3516 -0.6461 -0.2934 0.2344 3.0087
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.550059 0.618178 -2.507 0.0122 *
x1 0.034636 0.017351 1.996 0.0459 *
x2 0.090290 0.122838 0.735 0.4623
x3 -0.257532 0.033096 -7.781 7.17e-15 ***
x4 -0.104765 0.023203 -4.515 6.33e-06 ***
x5 -0.009071 0.007743 -1.172 0.2414
x6 0.067232 0.030289 2.220 0.0264 *
x7 0.615093 0.113216 5.433 5.54e-08 ***
x8 0.068376 0.077013 0.888 0.3746
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 801.68 on 698 degrees of freedom
Residual deviance: 551.00 on 690 degrees of freedom
(1 observation deleted due to missingness)
AIC: 569
Number of Fisher Scoring iterations: 6
采用逐步尋優剔除變量,消除多重共線性,構建新的模型,選模型的AIC值為最小值,采用R語言自帶的后向選擇函數可以得到同樣的模型,自帶的前向選擇函數得到有全部自變量的全模型,以此,選擇最優的模型。
看完上述內容,你們掌握R語言中基于Logistic銀行貸款拖欠率用戶分析是怎樣的的方法了嗎?如果還想學到更多技能或想了解更多相關內容,歡迎關注億速云行業資訊頻道,感謝各位的閱讀!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。