您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
小編給大家分享一下Matlab如何實現基于AHP高校食堂滿意度調查示例,相信大部分人都還不怎么了解,因此分享這篇文章給大家參考一下,希望大家閱讀完這篇文章后大有收獲,下面讓我們一起去了解一下吧!
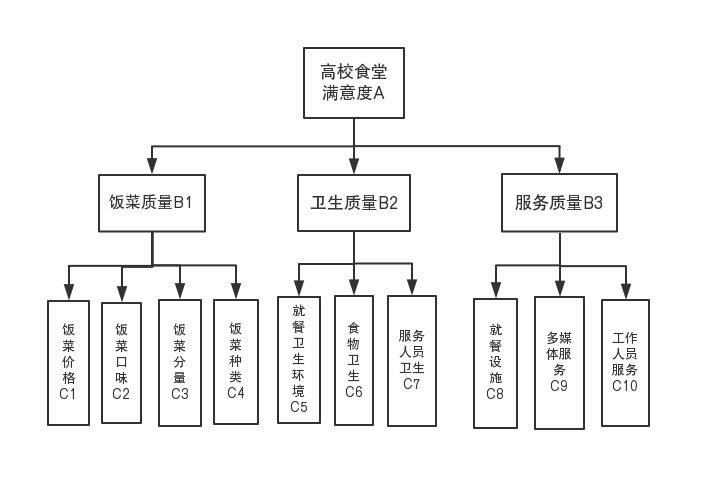
本研究采用的滿意度指標體系是項目組運用深度訪談和小組訪談法經過業內專家反復論證篩選確立的,能綜合反映高校食堂的滿意度水平,在深入分析高校食堂滿意度的問題上,將有關影響因素,按照層次模型,根據隸屬關系,分為若干個層次,高校食堂滿意度A為目標層,飯菜質量B1,衛生質量B2,服務質量B3為準則層,接下來,飯菜價格C1,飯菜口味C2,飯菜分量C3,飯菜種類C4,就餐衛生環境C5,食物衛生C6,服務人員衛生C7,就餐設施C8,多媒體服務C9,工作人員服務C10為對應下的方案層。
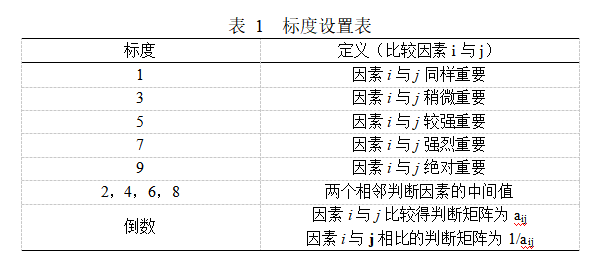

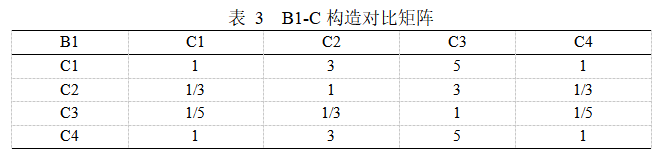

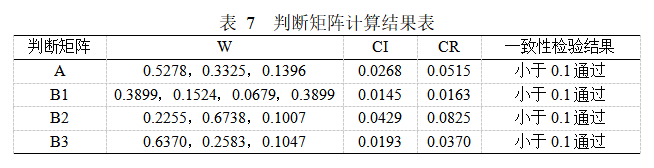
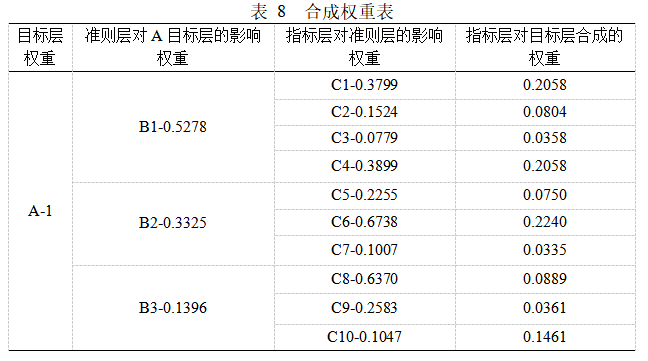
同理可得,判斷矩陣B1的特征向量為W=(0.3899,0.1524,0.0679,0.3899),表示對于準則層B1(飯菜質量),方案層C1(飯菜價格),C2(飯菜口味),C3(飯菜分量),C4(飯菜種類)的相對權重值分別為0.3899,0.1524,0.0679,0.3899。
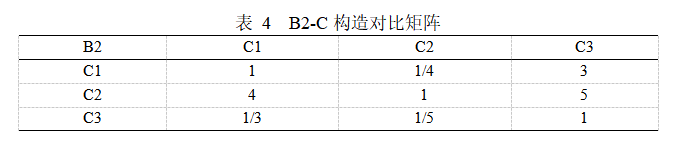
判斷矩陣B2的特征向量為W=(0.2255,0.6738,0.1007),表示對于準則層B2(衛生質量),方案層C5(就餐衛生環境)C6(食物衛生)C7(服務人員衛生)的相對權重值分別為0.2255,0.6738,0.1007。
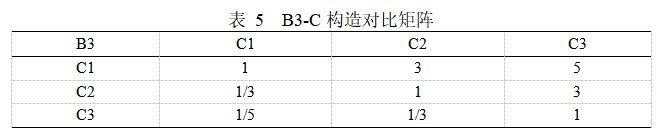
判斷矩陣B3的特征向量為W=(0.6370,0.2583,0.1047),表示對于準則層B3(服務質量),方案層C8(就餐設施),C9(多媒體服務),C10(工作人員服務)的相對權重值分別為0.6370,0.2583,0.1047。
以矩陣A為例進行一致性檢驗:CI=0.0268,CR=0.0515<0.1,由此斷定判斷矩陣A具有滿意的一致性,該判斷矩陣為有效矩陣,是可以用來做層次分析的。同理,對判斷矩陣B1,B2,B3,進行一致性檢驗,得到三個判斷矩陣的CR值分別為0.0163,0.0825,0.0370均小于0.1,因此斷定這三個判斷矩陣均通過一致性檢驗,均為有效矩陣。
%層次分析法(AHP)disp('請輸入判斷矩陣A(n階)');A = input('A=');[n,n] = size(A);x = ones(n,100);y = ones(n,100);m = zeros(1,100);m(1) = max(x(:,1));y(:,1) = x(:,1);x(:,2) = A*y(:,1);m(2) = max(x(:,2));y(:,2) = x(:,2)/m(2);p=0.0001; i=2; k=abs(m(2)-m(1));while k>p i=i+1; x(:,i) = A*y(:,i-1); m(i) = max(x(:,i)); y(:,i) = x(:,i)/m(i); k=abs(m(i)-m(i-1));enda = sum(y(:,i));w = y(:,i)/a;t = m(i);disp(w);%一致性檢驗CI = (t-n)/(n-1);RI = [0 0 0.52 0.89 1.12 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];CR = CI/RI(n);if CR<0.10 disp('此矩陣一致性可以接受!'); disp('CI=');disp(CI); disp('CR=');disp(CR);end
以上是“Matlab如何實現基于AHP高校食堂滿意度調查示例”這篇文章的所有內容,感謝各位的閱讀!相信大家都有了一定的了解,希望分享的內容對大家有所幫助,如果還想學習更多知識,歡迎關注億速云行業資訊頻道!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。