Python如何實現異常檢測

本文小編為大家詳細介紹“Python如何實現異常檢測”，內容詳細，步驟清晰，細節處理妥當，希望這篇“Python如何實現異常檢測”文章能幫助大家解決疑惑，下面跟著小編的思路慢慢深入，一起來學習新知識吧。

異常檢測算法

我將使用Andrew Ng的機器學習課程的數據集，它具有兩個訓練特征。我沒有在本文中使用真實的數據集，因為這個數據集非常適合學習。它只有兩個特征。在任何真實的數據集中，都不可能只有兩個特征。

首先，導入必要的包

import pandas as pd  import numpy as np

導入數據集。這是一個excel數據集。在這里，訓練數據和交叉驗證數據存儲在單獨的表中。所以，讓我們把訓練數據帶來。

df = pd.read_excel('ex8data1.xlsx', sheet_name='X', header=None) df.head()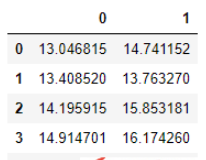

讓我們將第0列與第1列進行比較。

plt.figure() plt.scatter(df[0], df[1]) plt.show()

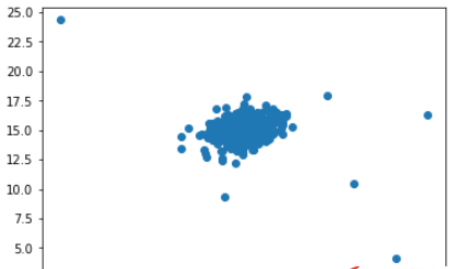
你可能通過看這張圖知道哪些數據是異常的。

檢查此數據集中有多少個訓練示例：

m = len(df)

計算每個特征的平均值。這里我們只有兩個特征：0和1。

s = np.sum(df, axis=0) mu = s/m mu

輸出：

0    14.112226 1    14.997711 dtype: float64

根據上面“公式和過程”部分中描述的公式，讓我們計算方差：

vr = np.sum((df - mu)**2, axis=0) variance = vr/m variance

輸出：

0    1.832631 1    1.709745 dtype: float64

現在把它做成對角線形狀。正如我在概率公式后面的“公式和過程”一節中所解釋的，求和符號實際上是方差

var_dia = np.diag(variance) var_dia

輸出：

array([[1.83263141, 0.        ],        [0.        , 1.70974533]])

計算概率：

k = len(mu) X = df - mu p = 1/((2*np.pi)**(k/2)*(np.linalg.det(var_dia)**0.5))* np.exp(-0.5* np.sum(X @ np.linalg.pinv(var_dia) * X,axis=1)) p

訓練部分已經完成。

下一步是找出閾值概率。如果概率低于閾值概率，則示例數據為異常數據。但我們需要為我們的特殊情況找出那個閾值。

對于這一步，我們使用交叉驗證數據和標簽。

對于你的案例，你只需保留一部分原始數據以進行交叉驗證。

現在導入交叉驗證數據和標簽：

cvx = pd.read_excel('ex8data1.xlsx', sheet_name='Xval', header=None) cvx.head()

標簽如下：

cvy = pd.read_excel('ex8data1.xlsx', sheet_name='y', header=None) cvy.head()

我將把'cvy'轉換成NumPy數組，因為我喜歡使用數組。不過，數據幀也不錯。

y = np.array(cvy)

輸出：

# 數組的一部分 array([[0],        [0],        [0],        [0],        [0],        [0],        [0],        [0],        [0],

這里，y值0表示這是一個正常的例子，y值1表示這是一個異常的例子。

現在，如何選擇一個閾值？

我不想只檢查概率表中的所有概率。這可能是不必要的。讓我們再檢查一下概率值。

p.describe()

輸出：

count    3.070000e+02 mean     5.905331e-02 std      2.324461e-02 min      1.181209e-23 25%      4.361075e-02 50%      6.510144e-02 75%      7.849532e-02 max      8.986095e-02 dtype: float64

如圖所示，我們沒有太多異常數據。所以，如果我們從75%的值開始，這應該是好的。但為了安全起見，我會從平均值開始。

因此，我們將從平均值和更低的概率范圍。我們將檢查這個范圍內每個概率的f1分數。

首先，定義一個函數來計算真正例、假正例和假反例：

def tpfpfn(ep):     tp, fp, fn = 0, 0, 0     for i in range(len(y)):         if p[i] <= ep and y[i][0] == 1:             tp += 1         elif p[i] <= ep and y[i][0] == 0:             fp += 1         elif p[i] > ep and y[i][0] == 1:             fn += 1     return tp, fp, fn

列出低于或等于平均概率的概率。

eps = [i for i in p if i <= p.mean()]

檢查一下列表的長度

len(eps)

輸出：

133

根據前面討論的公式定義一個計算f1分數的函數：

def f1(ep):     tp, fp, fn = tpfpfn(ep)     prec = tp/(tp + fp)     rec = tp/(tp + fn)     f1 = 2*prec*rec/(prec + rec)     return f1

所有函數都準備好了！

現在計算所有epsilon或我們之前選擇的概率值范圍的f1分數。

f = [] for i in eps:     f.append(f1(i)) f

輸出：

[0.14285714285714285,  0.14035087719298248,  0.1927710843373494,  0.1568627450980392,  0.208955223880597,  0.41379310344827586,  0.15517241379310345,  0.28571428571428575,  0.19444444444444445,  0.5217391304347826,  0.19718309859154928,  0.19753086419753085,  0.29268292682926833,  0.14545454545454545,

這是f分數表的一部分。長度應該是133。

f分數通常在0到1之間，其中f1得分越高越好。所以，我們需要從剛才計算的f分數列表中取f的最高分數。

現在，使用“argmax”函數來確定f分數值最大值的索引。

np.array(f).argmax()

輸出：

131

現在用這個索引來得到閾值概率。

e = eps[131] e

輸出：

6.107184445968581e-05

找出異常實例

我們有臨界概率。我們可以從中找出我們訓練數據的標簽。

如果概率值小于或等于該閾值，則數據為異常數據，否則為正常數據。我們將正常數據和異常數據分別表示為0和1，

label = [] for i in range(len(df)):     if p[i] <= e:         label.append(1)     else:         label.append(0) label

輸出：

[0,  0,  0,  0,  0,  0,  0,  0,  0,  0,

這是標簽列表的一部分。

我將在上面的訓練數據集中添加此計算標簽：

df['label'] = np.array(label) df.head()

我在標簽為1的地方用紅色繪制數據，在標簽為0的地方用黑色繪制。以下是結果。

讀到這里，這篇“Python如何實現異常檢測”文章已經介紹完畢，想要掌握這篇文章的知識點還需要大家自己動手實踐使用過才能領會，如果想了解更多相關內容的文章，歡迎關注億速云行業資訊頻道。