您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“怎么使用numpy實現LR算法”,在日常操作中,相信很多人在怎么使用numpy實現LR算法問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”怎么使用numpy實現LR算法”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
問題: 如果給你一個給你 1000000 個數據 a1~a1000000,以及 1000000 個數據 b1~b1000000,要你求每一對 ai 和 bi 相乘的結果的總和c,你會怎么做?
采用for循環累加的代碼如下
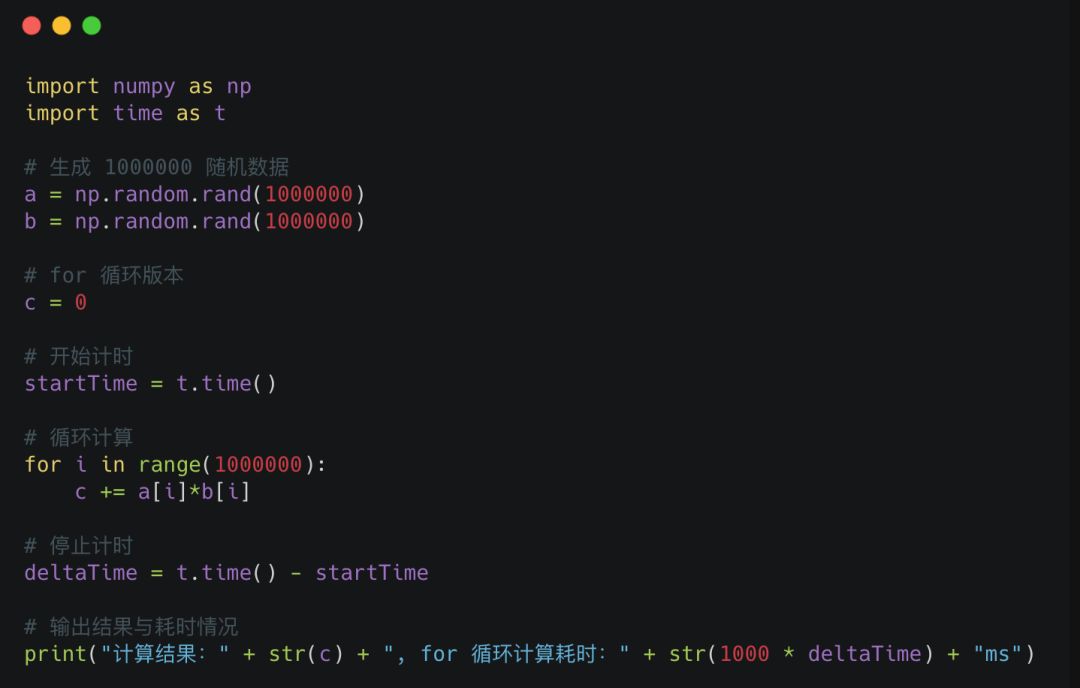
計算結果:249879.05298545936, for 循環計算耗時:519.999980927ms
如果采用numpy來進行同等的操作(向量化)

計算結果:249879.05298545936, 矩陣計算耗時:0.999927520752ms
這計算速度的差距比馬里亞納海溝還深, 之所以差距會這么大, 是因為numpy, matlab這類矩陣運算的程序, 充分利用了現代CPU的SIMD技術, 極大提高了運算效率
現在我們拿最簡單的LR邏輯回歸來講一下, 如何使用向量化的技巧, 手動訓練模型
假如我們選用 BGD(批量梯度下降) 或者 MBGD(小批量梯度下降), 那么LR的參數訓練公式為

可以看到, 上述推導的公式中,中間的那個大矩陣, 其實就是輸入數據矩陣的轉置,這樣代碼實現就很簡單了, 使用numpy實現的LR算法為
def grand_ascent(data_train, data_label):
dataMatrix = np.mat(data_train)
labelMat = np.mat(data_label).transpose()
m, n = np.shape(dataMatrix)
weights = np.ones((n, 1))
alpha = 0.001
for i in range(0, 500):
h = sigmoid(dataMatrix * weights)
weights = weights + alpha * dataMatrix.transpose() * (labelMat - h)
return weights到此,關于“怎么使用numpy實現LR算法”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。