Sklearn廣義線性模型實例分析

這篇文章主要介紹了Sklearn廣義線性模型實例分析的相關知識，內容詳細易懂，操作簡單快捷，具有一定借鑒價值，相信大家閱讀完這篇Sklearn廣義線性模型實例分析文章都會有所收獲，下面我們一起來看看吧。

廣義線性模型：主要講述一些用于回歸的方法，其中目標值y是輸入變量x的線性組合。數據概念表示為：如果y(w,x)=w0+w1x1+...+wpxp,在整個模塊中，我們定義向量w=(w1,...,wp)作為coef_，定義w0作為intercept_。

1.1.1.普通最小二乘法
LinearRegression擬合一個帶有系數w=(w1,...,wp)的線性模型，使得數據集實際觀測數據和預測數據（估計值）之間的殘差平方和最小。其數學表達式為:

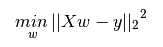
LinearRegression會調用fit方法來擬合數組 X,y,并且將線性模型的系數w存儲在其成員變量coef_中:

>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> reg.coef_
array([ 0.5,  0.5])

然而，對于普通最小二乘的系數估計問題，其依賴于模型各項的相互獨立性。當各項是相關的，且設計矩陣X的各列近似線性相關，那么，設計矩陣會趨向于奇異矩陣，這種特性導致最小二乘估計對于隨機誤差非常敏感，可能產生很大的方差。例如，在沒有實驗設計的情況下收集到的數據，這種多重共線性（multicollinearity）的情況可能真的會出現。

線性回歸示例：

本示例僅使用糖尿病數據集的第一個特征，以說明此回歸技術的二維圖。 可以在圖中看到直線，該直線顯示了線性回歸如何嘗試繪制一條直線，該直線將最大程度地減少數據集中觀察到的響應與線性近似預測的響應之間的殘差平方和。還計算輸出了系數，殘差平方和和方差得分。

import matplotlib.pyplot as pltimport numpy as npfrom sklearn import datasets, linear_modelfrom sklearn.metrics import mean_squared_error, r2_scoreimport pandas as pd#加載數據diabetes = datasets.load_diabetes()
# 取一個特征列維度diabetes_X = diabetes.data[:, np.newaxis, 2]#np.newaxis將矩陣轉換成一列# 劃分訓練和測試數據集diabetes_X_train = diabetes_X[:-20]diabetes_X_test = diabetes_X[-20:]
# 劃分訓練和測試目標集diabetes_y_train = diabetes.target[:-20]diabetes_y_test = diabetes.target[-20:]
# 創建線性回歸模型regr = linear_model.LinearRegression()
# 使用數據集訓練模型regr.fit(diabetes_X_train, diabetes_y_train)
# 使用測試集訓練函數diabetes_y_pred = regr.predict(diabetes_X_test)
# 系數print('Coefficients: \n', regr.coef_)# 平均誤差print("Mean squared error: %.2f"% mean_squared_error(diabetes_y_test, diabetes_y_pred))# 變量預測分數print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))
# 可視化輸出plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')plt.plot(diabetes_X_test, diabetes_y_pred, color='red', linewidth=3)
#橫縱坐標plt.xticks(())plt.yticks(())
plt.show()

輸出：

Coefficients:
 [938.23786125]
Mean squared error: 2548.07
Variance score: 0.47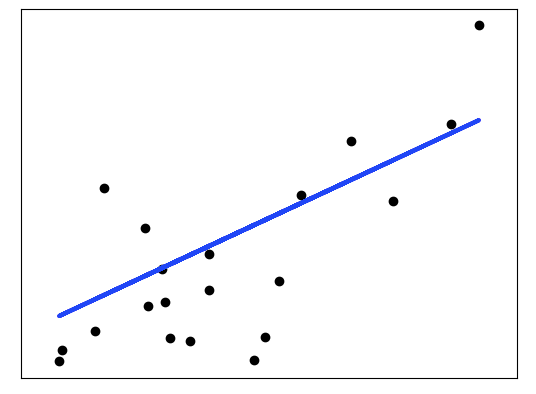

關于“Sklearn廣義線性模型實例分析”這篇文章的內容就介紹到這里，感謝各位的閱讀！相信大家對“Sklearn廣義線性模型實例分析”知識都有一定的了解，大家如果還想學習更多知識，歡迎關注億速云行業資訊頻道。