您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家介紹大數據中如何使用Q-Q圖驗證數據的分布,內容非常詳細,感興趣的小伙伴們可以參考借鑒,希望對大家能有所幫助。
Q-Q圖是檢驗任何隨機變量(如正態分布、指數分布、對數正態分布等)分布的圖形方法,是觀察任何分布性質的一種統計方法。
例如,如果給定的一個分布需要驗證它是否是正態分布,我們運行統計分析并將未知分布與已知正態分布進行比較。然后通過觀察Q-Q圖的結果,我們可以確定給定的分布是否正態分布。
給定一個未知的隨機變量。
找到每個百分位值
生成一個已知的隨機分布,根據該分布同樣遵循步驟1-2。
繪制Q-Q圖
給定一個隨機分布,需要驗證它是否為正態/高斯分布。為了便于理解,我們將這個未知分布命名為X,將已知的正態分布命名為Y。
X = np.random.normal(loc=50, scale=25, size=1000)
我們正在生成一個正態分布,有1000個值,平均值=50,標準差=25。
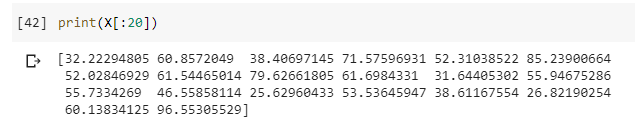
查找1%~100%:
X_100 = [] for i in range(1,101): X_100.append(np.percentile(X, i))
計算每個百分位數(1%,2%,3%,. . .,99%,100%)X的隨機分布值,并將其存儲在X_100中。
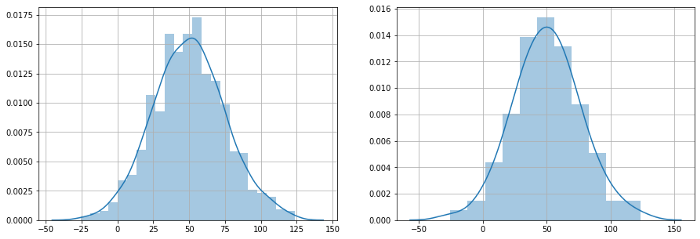
Y = np.random.normal(loc=0, scale=1, size=1000)
生成一個正態分布,其平均值為0,標準偏差為1,需要與未知分布X進行比較,以驗證X分布是否正態分布。
Y_100 = [] for i in range(101): Y_100.append(np.percentile(Y, i))
計算每個百分位數(1%,2%,3%,. . .,99%,100%)Y的隨機分布值,并將其存儲在Y_100中。
為以上獲得的未知分布值繪制散點圖。
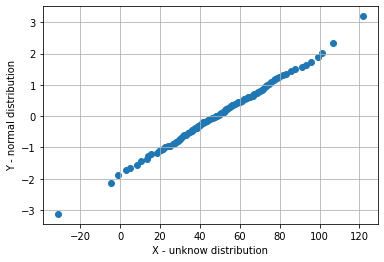
這里X是未知分布,要與Y這個正態分布相比。
對于Q-Q圖,如果圖中的散點在一條直線上,則兩個隨機變量具有相同的分布,否則它們具有不同的分布。
從上面的Q-Q圖可以看出X是正態分布的。

如果X不是正態分布,并且它有其他分布,那么如果Q-Q圖是在X和正態分布之間繪制的,那么散射點就不會在一條直線上。
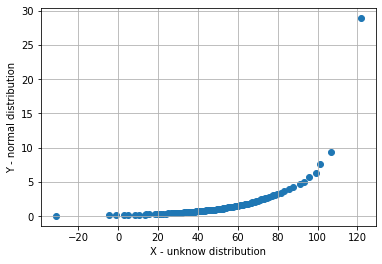
這里,X分布是對數正態分布,因此Q-Q圖中的散射點不是直線。
這是4個不同條件下X和Y分布的Q-Q圖。
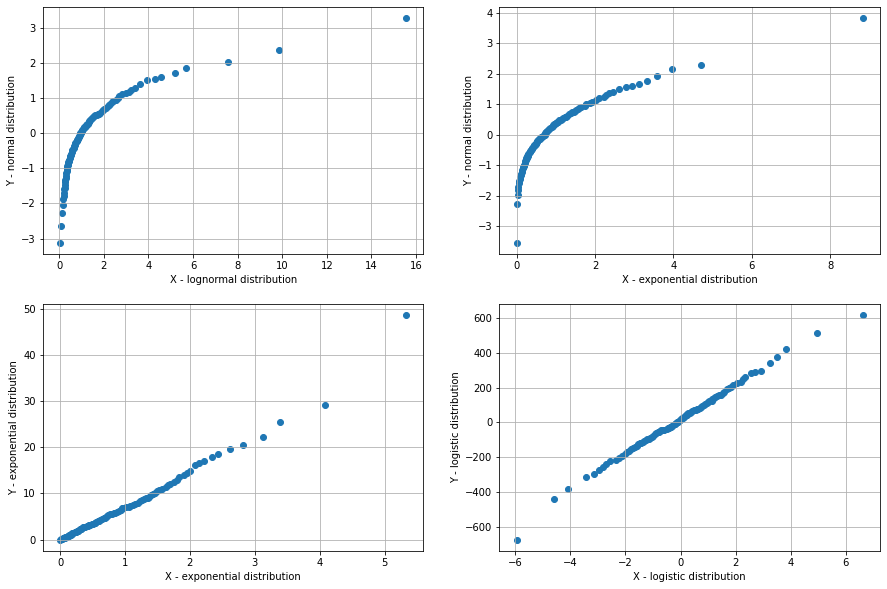
左上:對數正態分布與正態分布的QQ圖
右上:正態與指數分布的QQ圖
左下:指數與指數分布的QQ圖
右下:logistic與logistic分布的QQ圖
import numpy as np
import matplotlib.pyplot as plt
X = np.random.normal(loc=50, scale=25, size=1000)
X_100 = []
for i in range(1,101):
X_100.append(np.percentile(X, i))
Y = np.random.normal(loc=0, scale=1, size=1000)
Y_100 = []
for i in range(1,101):
Y_100.append(np.percentile(Y, i))
plt.scatter(X_100, Y_100)
plt.grid()
plt.ylabel("Y - normal distribution")
plt.xlabel("X - normal distribution")
plt.show()Q-Q圖可以用來比較任意兩個分布,并且可以通過與已知分布的比較來驗證未知分布。這種方法有一個主要的局限性,即需要大量的數據點,因為得出較少的數據不是明智的決定。通過觀察Q-Q圖可以預測這兩種分布是否相同。
關于大數據中如何使用Q-Q圖驗證數據的分布就分享到這里了,希望以上內容可以對大家有一定的幫助,可以學到更多知識。如果覺得文章不錯,可以把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。