怎樣解析Unity3D骨骼動畫原理的學習

本篇文章給大家分享的是有關怎樣解析Unity3D骨骼動畫原理的學習，小編覺得挺實用的，因此分享給大家學習，希望大家閱讀完這篇文章后可以有所收獲，話不多說，跟著小編一起來看看吧。

最近研究了一下游戲中模型的骨骼動畫的原理，做一個學習筆記，便于大家共同學習探討。

一、骨骼動畫、關節動畫、關鍵幀動畫

在實際的游戲中，用的最多的是這三種基本的動畫。

在關鍵幀動畫中，模型在每個關鍵幀中都是一個固定的姿勢，相當于一個“快照”，通過在不同的關鍵幀中進行插值平滑計算，可以得到一個較為流暢的動畫表現。關鍵幀動畫的一個優勢是只需要做插值計算，相對于其他的動畫計算量很小，但是劣勢也比較明顯，基于固定的“快照”進行插值計算，表現大大被限制，同時插值如果不夠平滑容易出現尖刺等現象。

關節動畫是早期出現的一種動畫，在這種動畫中，模型整體不是一個Mesh, 而是分為多個Mesh，通過父子的關系進行組織，這樣父節點的Mesh就會帶動子節點的Mesh進行變換，這樣層層的變換關系，就可以得到各個子Mesh在不同關鍵幀中的位置。關節動畫相比于關鍵幀動畫，依賴于各個關鍵幀的動畫數據，可以實時的計算出各個Mesh的位置，不再受限于固定的位置，但是由于是分散的各個Mesh，這樣在不同Mesh的結合處容易出現裂縫。

骨骼動畫是進一步的動畫類型，原理構成極其簡單，但是解決問題極其有優勢。將模型分為骨骼Bone和蒙皮Mesh兩個部分，其基本的原理可以闡述為：模型的骨骼可分為基本多層父子骨骼，在動畫關鍵幀數據的驅動下，計算出各個父子骨骼的位置，基于骨骼的控制通過頂點混合動態計算出蒙皮網格的頂點。在骨骼動畫中，通常包含的是骨骼層次數據，網格Mesh數據， 網格蒙皮數據Skin Info和骨骼的動畫關鍵幀數據。

二、SkinnedMesh動畫原理分析

對于Skinned Mesh的理解關鍵是蒙皮的計算過程，這里的皮，并不是我們常見的在shader中用到的貼圖texture，而是模型的mesh, 所以蒙皮其實就是計算mesh相對于骨骼的位置變換過程。如果我們的骨骼沒有變化，那么我們的mesh就沒有變化，此時的mesh就相當于一個靜態的mesh。所以對于skinned的理解，就是指具有蒙皮數據skin info的mesh :D。 在實際的實例中，skin info主要包含當前mesh上的頂點受到哪些骨骼影響，各個骨骼的影響權重。借用文章1中的表述，整個mesh頂點的變換過程可以用矩陣的方式表述：

V_world = V_mesh * BoneOffsetMatrix₁ * CombineMatrix₁ * W₁ +V_mesh * BoneOffsetMatrix₂ * CombineMatrix₂ * W₂ +...+ V_mesh * BoneOffsetMatrix_n * CombineMatrix_n * W_n

其中BoneOffsetMatrix 和 CombineMatrix在下面的講解中會詳細講解求解過程。

 1、骨骼動畫中的骨骼

在我們常見的模型建模中，美術通常將模型設置成雙手水平，雙腿分立的類“大”字型。 為什么要用這樣的方式？ 這與我們的模型的骨骼有一定的關系。通常模型骨骼數量都有一個限制（通常為30，下面會解釋為什么受到限制），模型不可能為一根骨骼，如果為一根骨骼，那么模型的表現就會顯得比較單一，想要表現出類似于人體的動畫，一般都會有多個骨骼。對于每個骨骼，如何建立其組織關系，在建模的時候就進行了基本的設定。通常美術會選擇模型的盆骨做為模型的根骨骼，那么基于根骨骼，可以遞推出各個骨骼相對于根骨的父子關系。通過骨骼所在的空間，其原點我們會選擇兩個腳之間的中點作為原點，這時候就會發現根骨骼并沒有和原點重合，這時美術會構建一個Scene_Root做為額外的骨骼，其位置就為世界原點，而真正的根骨骼Bip01會作為Scene_Root的唯一子骨骼。

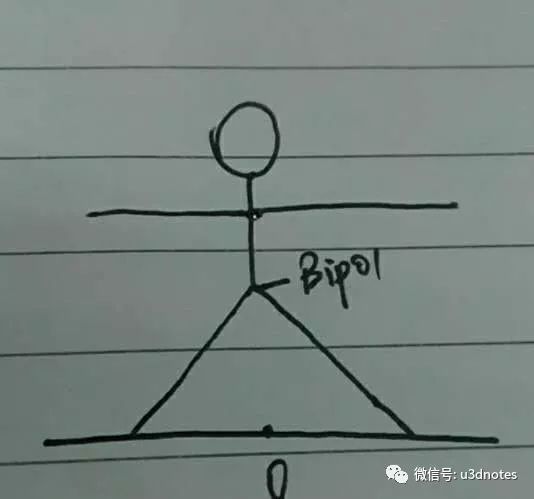
請忽略我的靈魂畫法:D

基于根骨骼，我們可以遞推出各個骨骼相對于根骨骼的父子轉換矩陣，通常這樣的矩陣轉換為旋轉矩陣，不存在平移和縮放，當然比如你的一個模型動畫是拉長模型的身體（比如海賊王這種動畫:D），那么你可以添加平移和縮放到變換矩陣中。此時對于整個模型就有了一個基本的直觀的感受了，模型的具體動畫，取決于模型的骨骼，牽一發而動全身，整個模型的運動會帶動外面的mesh一起運動，就可以表現出整個模型的骨骼動畫，這樣，我們對于骨骼動畫就有一個基本的理解。

借用參考文1的說話，骨骼的本質，其實就是一個坐標空間，我們在做骨骼動畫的時候，關鍵幀中包含的對骨骼的變換主要為旋轉矩陣，所以對骨骼的變換就是對骨骼空間的旋轉變換。說簡單點，一個骨骼動畫，帶來的變換，首先作用在根骨骼上，影響根骨骼的坐標空間，然后遞歸的影響根骨的子骨骼，這樣層層的遞歸影響，最后帶來的就是整體骨骼變換。基于此，我們就可以理解關節的作用，關節就是骨骼自身空間的原點。關節的位置由當前骨骼在其父節點骨骼空間中的位置來描述，繞關節的旋轉就是骨骼空間自身的旋轉，這樣變換就通過關節層層遞歸傳遞。用c++的表述，可以定義一個基本的骨骼類，主要包含自己的世界坐標中的位置，在父節點中的位置，其第一個子節點，其兄弟骨骼的指針，代碼依據于文章1：

class Bone
{
   Bone* m_pFirstChild;  
   Bone* m_pSibling;
   float m_x, m_y, m_z; // pos in parents' space
   float m_wx, m_wy, m_wz; // pos in world space
  //
  public:
  Bone(float x, float y, float z): m_pSibling(NULL),m_pFirstChild(NULL),m_pFather(NULL),m_x(x), m_y(y), m_z(z){}

  //
  void SetFirstChild(Bone* pChild)
  {
      m_pFirstChild = pChild;
      m_pFirstChild->m_pFather = this;
  }
  //
   void SetSibling(Bone* pSibling)
   {
      m_pSibling = pSibling;
      m_pSibling->m_pFather = m_pFather;
    }
}

這樣，當父節點骨骼發生變換的時候，子節點的骨骼就會做相應的變換，這樣的操作可以稱為 UpdateBoneMatrix，這樣的操作可以用一個方法ComputeWorldPos來表示，這樣可以用遞歸的方式在Bone中實現，代碼依據于文章1：

class Bone
{
    void ComputeWorldPos(float fatherX, float fatherY, float fatherZ)
    {
         m_wx = fatherX + m_x;
         m_wy = fatherY + m_y;
         m_wz = fatherZ + m_z;
        //兄弟節點用父節點傳遞的參數
        if(m_pSibling ！=NULL)
             m_pSibling ->ComputeWorldPos(fatherX, fatherY, fatherZ)
        if(m_pFirstChild!=NULL)
             m_pFirstChild ->ComputeWorldPos(m_wx, m_wy, m_wz)
    }
}

這樣，當父節點骨骼發生變換的時候，子節點的骨骼都會做出相應的變換，從而得到最新的位置、朝向等信息，骨骼發生變化，從而會帶動外在的mesh發生變化，所以整體的模型就表現chu出運動起來。基于此，可以理解為什么骨骼是骨骼動畫的核心。

2、骨骼動畫中的蒙皮

　　在說完骨骼后，對于整體模型在動畫中骨骼的變換，可以有一個大致的理解，當時模型只是內在的，外在的表現是模型的蒙皮的變化，所以骨骼動畫中的第二部分就是蒙皮的計算。這里的皮，就是前面說過的Mesh。

首先，需要明確的是Mesh所在的空間。在建模的時候，模型的Mesh是和骨骼一樣處于同樣的空間中的，Mesh中的各個頂點是基于Mesh的原點來進行定位的。但是模型在運動表現的時候，是根據骨骼的變換來做相應的動作的，對應的Mesh上的頂點就需要做出對應的轉換，所以Mesh的頂點需要轉換到對應的骨骼所在的坐標空間中，進行相應的位置變換，因此對應的需要添加蒙皮信息，也就是skin info，主要是當前頂點受到哪些骨骼的影響，影響的權重等，借用文章1的表述，可以用C++表示一個頂點類，代碼依據于文章1：

#define MAX_BONE_VERTEX 4
class Vertex
{
     float m_x, m_y, m_z; // local pos in mesh space
     float m_wx, m_wy, m_wz; // pos in world space
     //skin info
     int m_boneNum;
     Bone* m_bones[MAX_BONE_VERTEX];
     float m_boneWeights[MAX_BONE_VERTEX];
}

當然，這兒只是一個簡單的表述，具體的在引擎中會有規范的設計。那么我們的頂點在跟隨骨骼做運動的時候，是如何計算自己的位置的？我們就需要引入BoneOffsetMatrix 和 Transform Matrix的概念。

在前面，我們已經提到，頂點需要依附于骨骼進行位置計算，但是建模的時候，頂點的位置是基于Mesh原點進行建模的，通常情況下，Mesh的原點是和模型的骨骼的根骨骼處于同一個坐標空間中，那么 BoneOffsetMatrix就是用來將Mesh中頂點從Mesh空間轉換到骨骼所在空間中。

在建模的時候，對于每個骨骼，我們是可以得到其對應的Transform Matrix（用來層層計算到父節點所在空間中），其中根骨骼的Transform Matrix是基于世界空間的轉換，所以對于每一個下面的子骨骼，要計算其Transform Matrix，需要進行一個矩陣的連乘操作。最后得到的最終矩陣連乘結果矩陣就是Combined Transform Matrix，基于這個矩陣，就可以將頂點從骨骼所在的空間轉換到世界空間中。反過來，這個矩陣的逆矩陣（一般只考慮可以取逆的操作），就是從世界空間中轉換到該骨骼的空間中，由于Mesh的定義基于Mesh原點，Mesh原點就在世界空間中，所以這個逆矩陣就是要求的 Offset Matrix，也被稱為Inverse Matrix，這個逆矩陣一般實在初始位置中求得，通過取逆即可獲得。

在實際的計算中，每個骨骼可能會對應多個頂點，如果每個頂點都保存其對應的骨骼的變換矩陣，那么大量的頂點就會報錯非常多的變換矩陣。所以我們只需要保存當前該骨骼在初始位置，對應的從世界空間到其骨骼空間的變換矩陣，那么其對應的每個頂點在每次變換操作的時候，只需要對應的用offset Matrix來操作即可。

對于上面的Transform Matrix和offset Matrix，是納入了旋轉、平移和縮放的。其實offset Matrix取決于骨骼的初始位置，此時一般只包含了平移（此時還沒有動畫，所以沒有旋轉和縮放），在動畫中，一般也以縮放為主（所以大部分的動畫的關鍵幀用四元數表示）。在矩陣中都包含，是處于兼容性考慮。

這兒就基于平移，做一個基本的蒙皮的計算過程，代碼主要依據于文章1：

class BoneOffset
{
 public:
    float m_offx, m_offy, m_offz; //暫時只考慮平移
}

class Bone
{
   public :
       BoneOffset* m_boneOffset;
      //
      void ComputeBoneOffset()
      {
           m_boneOffset.m_offx -= m_wx;
           m_boneOffset.m_offy -= m_wy;
           m_boneOffset.m_offz -= m_wz;

            if(m_pSibling != NULL)
               m_pSibling->ComputeBoneOffset();
            if(m_pFirstChild !=NULL)
               m_pFirstChild->ComputeBoneOffset();
      }
}      

//頂點類的計算
class Vertex
{
 public:
     void ComputeWorldPosByBone(Bone* pBone, float &outX, float& outy, float& outz)
    {
   //從mesh空間轉換到bone空間
       outx = m_x + pBone->m_boneOffset.m_offx;
       outy = m_y + pBone->m_boneOffset.m_offy;
       outz = m_z + pBone->m_boneOffset.m_offz;
 //從bone空間轉換到世界空間
       outx += pBone->m_wx;
       outy += pBone->m_wy;
       outz += pBone->m_wz;
    }
    //GPU中計算頂點的位置
    void BlendVertex()
     ｛
       float m_wx = 0;
       float m_wy = 0;
       float m_wz = 0;
    
      for(int i=0; i < m_boneNum; i++)
       {
           float tx, ty,tz;           
           ComputeWorldPosByBone(m_bones[i], tx, ty,tz);

            tx *= m_boneWeights[i];
            ty *= m_boneWeights[i];
            tz *= m_boneWeights[i];
  
            m_wx += tx;
            m_wy += ty;
            m_wz += tz;
        }
     ｝

}

仔細捋一捋上面的代碼，就可以理解整體的蒙皮變換的過程，當然，這兒只用了矩陣變換中的平移變換，如果考慮加上旋轉和縮放，則回到最初的計算公式中了。至此，對于基本的骨骼動畫中的骨骼變換和蒙皮變換，有了一個詳細的解釋。下面說說Unity中是如何處理骨骼變換的。

三、Unity3D骨骼動畫處理

前面講解的對于骨骼動畫中的骨骼變換，蒙皮的計算，都是在CPU中進行的。在實際的游戲引擎中，這些都是分開處理的，較為通用的處理是將骨骼的動畫數據驅動放在CPU中，計算出骨骼的變換矩陣，然后傳遞給GPU中進行蒙皮計算。在DX10的時候，一般的shader給出的寄存器的大小在128的大小，一個變換矩陣為4x4，如果去除最后一行(0,0,0,1)就可以用3個float表示，那么最多可以表示，嗯，42個左右，如果考慮進行性能優化，不完全占用寄存器的大小，那么一般會限制在30根骨骼的大小上。將這些骨骼的變換矩陣在CPU進行計算后，就可以封裝成skin info傳遞到GPU中。

在GPU的計算中，就會取出這些mesh上的頂點進行對應的位置計算，基于骨骼的轉換矩陣和骨骼的權重，得到最新的位置，從而進行一次頂點計算和描繪。之所以將骨骼動畫的兩個部分分開處理，一個原因就是CPU的處理能力相對而言沒有GPU快捷，一般一個模型的骨骼數量是較小的，但是mesh上的頂點數量較大，利用GPU的并行處理能力優勢，可以分擔CPU的計算壓力。

在DX11還是DX12之后（記不太清楚），骨骼變換矩陣的計算結果不再存儲在寄存器中，而是存儲在一個buffer中，這樣的buffer大小基于骨骼數量的大小在第一次計算的時候設定，之后每次骨骼動畫數據驅動得到新的變換矩陣，就依次更改對應的buffer中存儲的變換矩陣，這樣就不再受到寄存器的大小而限制骨骼的根數的大小。但是實際的優化中，都會盡量優化模型的骨骼的數量，畢竟數量越多，特別是影響頂點的骨骼數量越多，那么計算量就會越大，正常的思維是優化骨骼數量而不是去擴展buffer的大小：D

在文章2中，對于GPU的蒙皮計算做了較大的性能優化，主要的思維也是這樣，在CPU中進行骨骼變換，將變換的結果傳遞到GPU中，從而進行蒙皮計算。基本的思維和前面說的變換思維一致，其基本的優化重點也是想利用一個buffer來緩存變換矩陣，從而優化性能。這兒我就重點分析一下shader部分的代碼，其在cpu部分的代碼處理基本和前面的代碼思想一致：

如果采用CPU的計算骨骼變換，那么GPU的shader:

uniform float4x4 _Matrices[24]; //設置的骨骼數量最大為24

struct appdata
{
    float4 vertex:POSITION;
    float2 uv:TEXCOORD0;
   //存儲的就是骨骼的變換矩陣，x/y為第一個骨骼的索引和權重，z/w為第二個的索引和權重
    float4 tangent:TANGENT;
}；

v2f vert(appdata v)
{
    v2f o;
    //蒙皮計算位置,注意看，其實就是矩陣變化加權重的表示
    float4 pos = 
    mul(_Matrices[v.tangent.x], v.vertex)* v.tangent.y +
    mul(_Matrices[v.tangent.z], v.vertex)* v.tangent.w
    //通用的mvp計算
    o.vertex = mul(UNITY_MATRIX_MVP, pos);
    o.uv  = TRANSFORM_TEX(v.uv, _MainTex);
    return o;
}

//怎么計算index和權重,此處一個蒙皮頂點受到2根骨骼的影響
Vector4[] tangents = new Vector4[mesh.vertexCount];
for(int i=0; i < mesh.vertexCount;++i)
{
   BoneWeight boneWeight = mesh.boneWeights[i];
   tangents[i].x = boneWeight.boneIndex0;
   tangents[i].y = boneWeight.weight0;
   tangents[i].z = boneWeight.boneIndex1;
   tangents[i].w = boneWeight.weight1;
}

newMesh.tangents = tangents;

其優化的策略，就是用貼圖的方式來存儲這個變換矩陣，參看一下代碼吧：

inline float4 indexToUV(int index)
{
    int row = (int) (index /_MatricesTexSize.x);
    int col   = (index - row * _MatricesTexsize.x; 
    return float4(col/_MatricesTexSize.x, row/_MatricesTexSize.y, 0 , 0);
}
//算出當前的變換矩陣
inline float4x4 getMatrix(int frameStartIndex, float boneIndex)
{
     int matStartIndex = frameStartIndex + boneIndex*3;
     float4 row0 = tex2Dlod(_MatricesTex, indexToUV(matStartIndx));
     float4 row1 = tex2Dlod(_MatricesTex, indexToUV(matStartIndx + 1));
     float4 row2 = tex2Dlod(_MatricesTex, indexToUV(matStartIndx + 2));
      float4 row3 = float4(0,0,0,0);
      float4x4 mat = float4x4(row0, row1, row2, row3);
      return mat;
}

v2f vert(appdata v)
{
     v2f o;
      float time = _Time.y;
     //算出當前時間對應的index
     int framIndex = (int)(((_Time.y + v.uv2.x)*_AnimFPS)%(_AnimLength * _AnimFPS));
     int frameStartIndex = frameIndex * _MatricesTexFrameTexls;
     //去除對應的變換矩陣
     float4 mat0 = getMatrix(frameStartIndex, v.tangent.x);
     float4 mat1 = getMatrix(frameStartIndex, v.tangent.z);
   
     float4 pos =
        mul(mat0, v.vertex) * v.tangent,y + 
        mul(mat1, v.vertex) * v.tangent.w;
 
    o.vertex = mul(UNITY_MATRIX_MVP, pos);
    o.uv = TRANSFOR_TEX(v.uv, _MainTex);
    return o;

以上就是怎樣解析Unity3D骨骼動畫原理的學習，小編相信有部分知識點可能是我們日常工作會見到或用到的。希望你能通過這篇文章學到更多知識。更多詳情敬請關注億速云行業資訊頻道。