Ceph分布式存儲糾刪碼之EC的示例分析

這篇文章給大家分享的是有關Ceph分布式存儲糾刪碼之EC的示例分析的內容。小編覺得挺實用的，因此分享給大家做個參考，一起跟隨小編過來看看吧。

1.副本orEC？

把一個文件放進磁盤很難嗎？不難，放進去就是了。

那么如果是特別重要的文件呢？也不難，多放幾份就是了。

還記得怎么對待畢業論文的嗎，電腦里存一份，U盤里存一份，網盤里再存一份，甚至好幾個網盤里都存一份。內心戰戰兢兢，生怕幾個月的努力（并沒有。。。）付諸東流。這，就是副本存儲。

假設我們的存儲是以三副本方式進行的話，我們可以計算出實際利用率是一個很低很低的值，33.3%。那么有沒有什么更好的辦法呢，有，就是糾刪碼的方案。

利用糾刪碼儲存文件，一共分三步:

• 把一個文件均分為K個數據塊

• 將這K個數據塊通過一定的方式聯系起來生成M個校驗塊

• 當某幾個數據塊丟失時，利用校驗塊重新計算出丟失的數據塊

以K，M取值為5、3為例，可以得出糾刪碼方案的利用率達到了5/8，62.5。在同樣可以容忍丟失三個數據塊的情況下，糾刪碼方案比副本方案容量利用率高出了近一倍！

可以看到重點就在于，如何計算出校驗塊以及如何利用其進行數據恢復，接下來就講重點介紹這兩部分，這，也就是EC的原理。

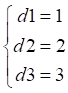
如果怕d1,d2,d3的某一個數據可能會丟失，那么我們就需要利用這三個數據通過計算來生成一個新的校驗數據。說白了，一個最簡單的方式就是，

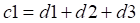
直接保存一個三者相加的值，那么當其中一個數據丟失，就可以通過c1減去另外兩個數據來進行恢復。

到此，一個最簡單的可以允許一個數據丟失的EC算法就構造成功了。

• 可以丟失兩個數據的EC算法

與丟失一個數據類似，我們會很容易想到，直接再構造一個校驗塊，比如，

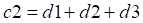
但是這樣真的可以嗎，仔細想來，這是個非常蠢的做法，如果真的丟失了兩個數據，這兩個一模一樣的方程根本無法解出兩個未知數，因為有兩個未知數但只有一個有效的方程。那么這兩個方程的系數向量有什么關系呢，這里引入一個線性代數的定義，它們線性相關。也就是說其中一個可以被另外一個線性表示。

知識點：線性相關。還不懂的同學自己回爐~

于是，我們可以改變c2方程的系數，隨便取一個，讓它和另一個線性無關，比如：

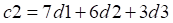
顯然，我們可以用初中一年級學到的解二元一次方程的方法輕易地將丟失的兩份數據恢復（就是解出來了那倆值）。

• EC算法推廣

如果，我們把上面的方程寫成矩陣乘法的形式，如下，

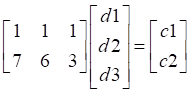
通過上文的分析，我們可以用非常樸素（low）的數學思想總結，當生成矩陣（就是校驗公式的系數矩陣）的行向量兩兩不相關時，生成的校驗數據可以在丟失數據時將其恢復。此時，如果我們回憶下大一的線性代數的知識，其實這就是要求生成矩陣可逆。

知識點：逆矩陣。

兩個矩陣相乘等于單位矩陣，就稱它們互為逆矩陣。

剛才我隨便取了c2的系數為7 6 3（其實是我的UM帳號后綴。。。），它恰巧是可行的，但是在有多個的情況下，需要有一個規律性的生成矩陣的取值，且保證這個矩陣可逆。比如，我們可以用下面這個規律，

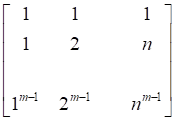
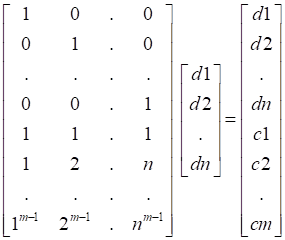
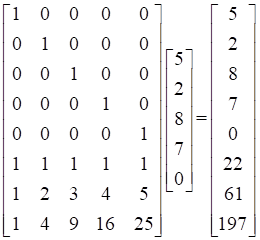
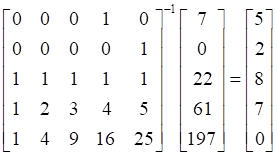
F = [0,0,0,1,0;0,0,0,0,1;1,1,1,1,1;1,2,3,4,5;1,4,9,16,25];
  F_INV = inv(F); %求F的逆矩陣
  C = [7;0;22;61;197];
  D = F_INV*C;
  D = 
      5.0000
      2.0000
      8.0000
      7.0000
           0

可以看到，丟失的數據得到了完美的還原。

感謝各位的閱讀！關于“Ceph分布式存儲糾刪碼之EC的示例分析”這篇文章就分享到這里了，希望以上內容可以對大家有一定的幫助，讓大家可以學到更多知識，如果覺得文章不錯，可以把它分享出去讓更多的人看到吧！