一個有趣的面試題：

假設當我們需要在一千萬個整數（整數的范圍在1-1億之間）里面快速查找某個整數是否存在于其中的話，如何快速查找進行判斷會比較方便呢？

ps: int 類型的數據存儲的時候是會占用四個字節空間，假設存儲的數據范圍在1-1億之間，那么數據存儲的時候大概占用空間為：100 * 100 * 1000 * 4 byte 大概存儲空間大小消耗為 ：40000 kb 40mb左右。

1.散列表結構方案

通過散列表來實現該功能當然是可以的，但是散列表里面除了需要存儲對應的數字以外，還需要存儲對應的鏈表指針，每個數字都采用int類型來進行存儲的話，光是數字占用的內存大小大概是40mb左右，如果是加上了指針的存儲空間的話，那么存儲的內存大小大概是80mb左右了。 

2.布爾數組結構方案

通過使用布爾類型的數組來進行存儲。首先創建一個一千萬長度的布爾類型數組，然后根據整數，定位到相應的下標賦值true，那么以后在遍歷的時候，根據相應的下標查找到指定的變量，如果該變量的值是true的話，那么就證明該數字存在。

布爾類型變量在存儲的時候只有true和false存在，但是在數組中存儲的時候實際上是占用了1個字節，該類型的變量在被編譯之后實際上是以int類型的數據0000 0000和0000 0001存儲的，因此還是占用了較多的內存空間。 

3.使用bitmap來進行存儲

例如說一個長度是10的bitmap，每一個bit位都存儲著對應的0到9的十個整形數字，此時每個bitmap所對應的位都是0。當我們存入的數字是3的時候，位于3的位置會變為1。

 

當我們存儲了多個數字的時候，例如說存儲了4,3,2,1的時候，那么位圖結構就會如下所示：

 

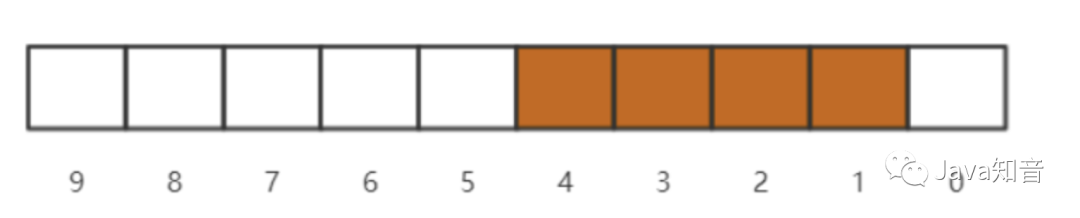
那么這個時候你可能就會疑惑了，到底在代碼上邊該如何通過計算來獲取一個數字的索引定位呢？

首先我們將核心思路的代碼先貼上來：

 public void set(int number) {
        //相當于對一個數字進行右移動3位，相當于除以8
        int index = number >> 3;
 
        //相當于 number % 8 獲取到byte[index]的位置
        int position = number & 0x07;
 
        //進行|或運算  參加運算的兩個對象只要有一個為1，其值為1。
        bytes[index] |= 1 << position;
    } 

為了方便理解核心思想，所以還是通過圖例來理解會比較好：

例如說往bitmap里面存儲一個數字11，那么首先需要通過向右移位（因為一個byte相當于8個bit），計算出所存儲的byte[]數組的索引定位，這里計算出index是1。由于一個byte里面存儲了八個bit位，所以通過求余的運算來計算postion，算出來為3。

這里假設原有的bitmap里面存儲了4和12這2個數字，那么它的結構如下所示：

 

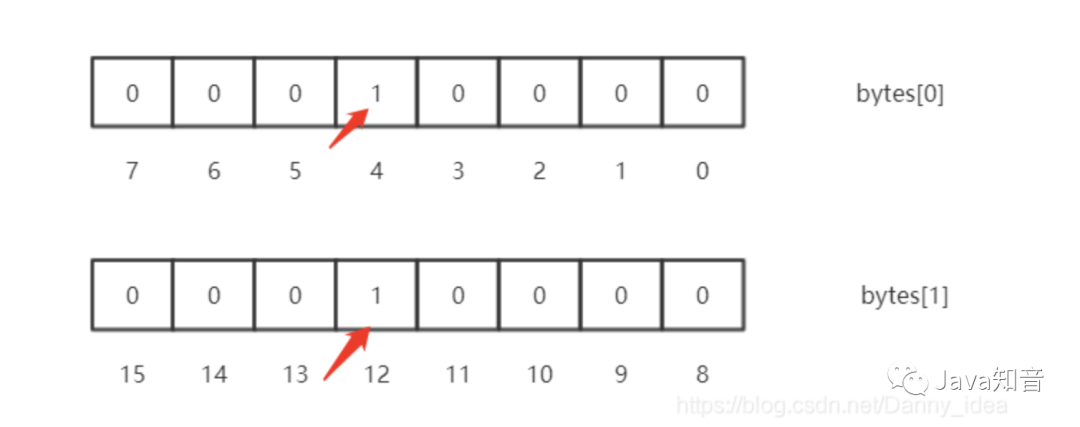
這個時候，我們需要存儲11進來，那么就需要進行或運算了：

 

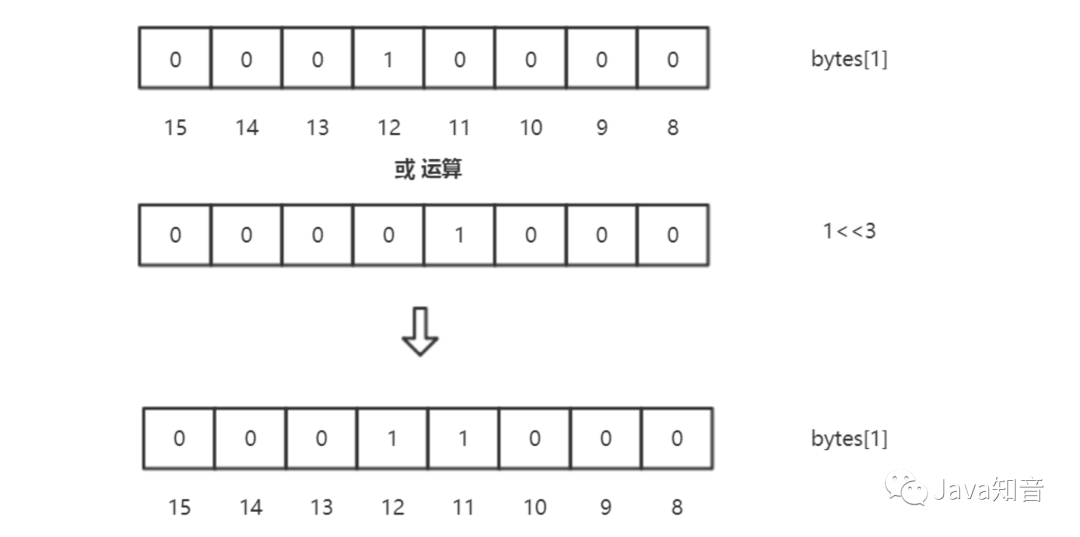
同理，當我們判斷數字是否存在的時候，也需要進行相應的判斷，代碼如下：

  public boolean contain(int number) {
        int index = number >> 3;
        int position = number & 0x07; 
        return (bytes[index] & (1<<position)) !=0;
    }

 

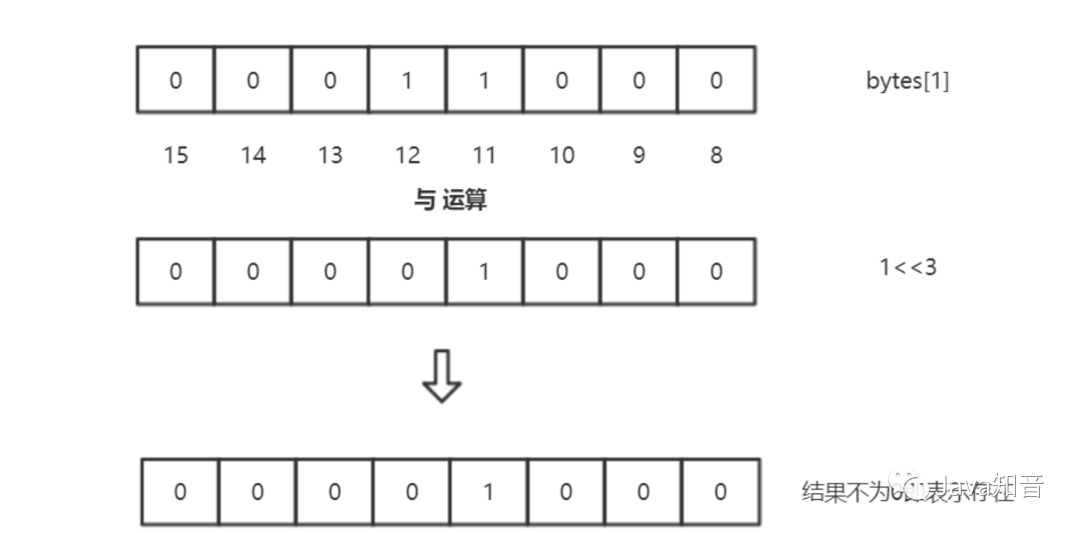
整合一下，簡單版的一個bitmap代碼如下：

public class MyBitMap {
 
    private byte[] bytes;
    private int initSize;
 
    public MyBitMap(int size) {
        if (size <= 0) {
            return;
        }
        initSize = size / (8) + 1;
        bytes = new byte[initSize];
    }
 
    public void set(int number) {
        //相當于對一個數字進行右移動3位，相當于除以8
        int index = number >> 3;
        //相當于 number % 8 獲取到byte[index]的位置
        int position = number & 0x07;
        //進行|或運算  參加運算的兩個對象只要有一個為1，其值為1。
        bytes[index] |= 1 << position;
    }
 
 
    public boolean contain(int number) {
        int index = number >> 3;
        int position = number & 0x07;
        return (bytes[index] & (1 << position)) != 0;
    }
 
    public static void main(String[] args) {
        MyBitMap myBitMap = new MyBitMap(32);
        myBitMap.set(30);
        myBitMap.set(13);
        myBitMap.set(24);
        System.out.println(myBitMap.contain(2));
    }
 
}

從剛剛位圖結構的講解中，你應該可以發現，位圖通過數組下標來定位數據，所以，訪問效率非常高。而且，每個數字用一個二進制位來表示，在數字范圍不大的情況下，所需要的內存空間非常節省。

比如剛剛那個例子，如果用散列表存儲這 1 千萬的數據，數據是 32 位的整型數，也就是需要 4 個字節的存儲空間，那總共至少需要 40MB 的存儲空間。如果我們通過位圖的話，數字范圍在 1 到 1 億之間，只需要 1 億個二進制位，也就是 12MB 左右的存儲空間就夠了。

但是實際應用中，卻并非如我們所想象的那么簡單，假設我們的實際場景進行改變一下：

還是剛剛的那個情況：

還是一千萬個數字，但是數字范圍不是 1 到 1 億，而是 1 到 10 億，那位圖的大小就是 10 億個二進制位，也就是 120MB 的大小，消耗的內存空間反而更加大了，而且在bitmap里面還會有部分空間浪費的情況存在。

假設我們對每一個數字都進行一次hash計算，然后通過hash將計算后的結果范圍限制在1千萬里面，那么就不需要再定義10億個二進制位了。

但是這樣子還是會有相應的弊端，例如說hash沖突。那么這個時候如果我們采用多個hash函數來進行處理的話，理論上是可以大大降低沖突的概率的。于是就有了下邊所說的布隆過濾器一說。

布隆過濾器

 

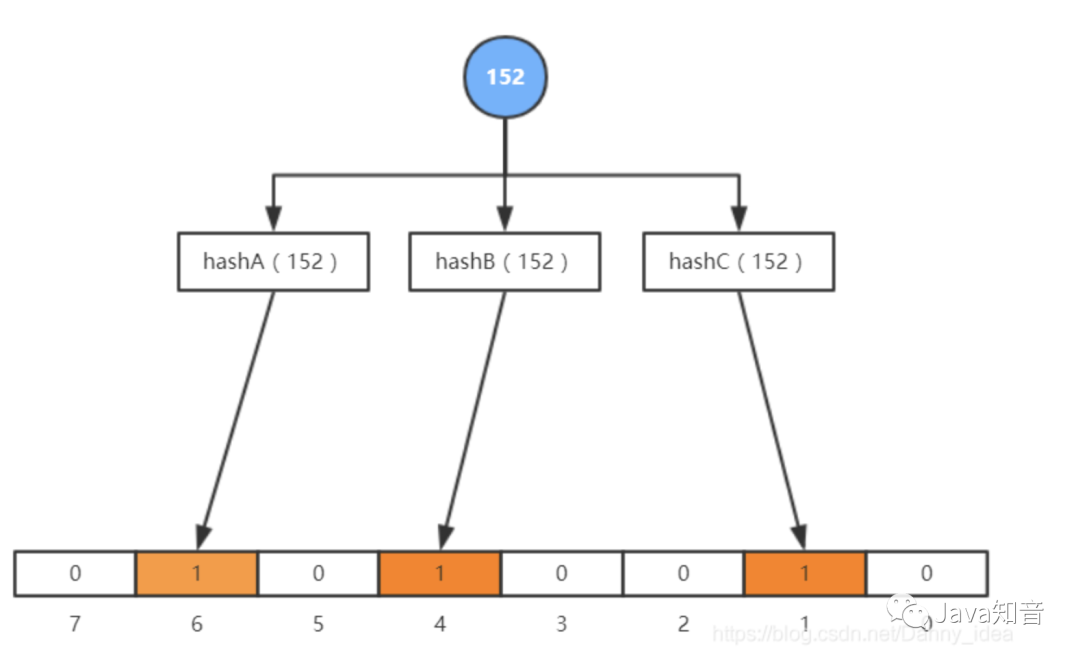
布隆過濾器通過使用多次的hash計算來進行數值是否存在的判斷，雖然大大降低了hash沖突的情況，但是還是存在一定的缺陷，那就是容易會有誤判的情況。例如說如下如所示：

 

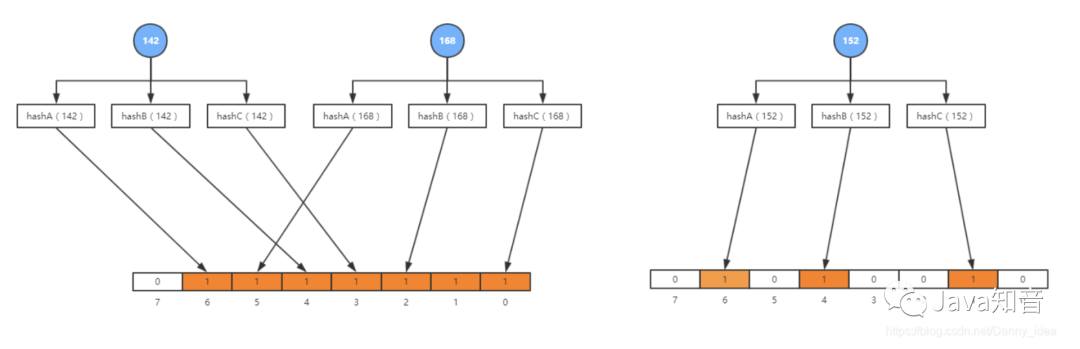
布隆過濾器的誤判有一個特點，那就是，它只會對存在的情況有誤判。如果某個數字經過布隆過濾器判斷不存在，那說明這個數字真的不存在，不會發生誤判；如果某個數字經過布隆過濾器判斷存在，這個時候才會有可能誤判，有可能并不存在。

不過，只要我們調整哈希函數的個數、位圖大小跟要存儲數字的個數之間的比例，那就可以將這種誤判的概率降到非常低。

那么該怎么調整這個位圖大小和存儲數字之間的比例呢？

這里可能就需要用到一些數學公式來進行計算了。

在位數組長度m的BF中插入一個元素，相應的位可能會被標志為1。所以說，在插入元素后，該比特仍然為0的概率是：

 

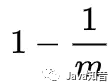
現有k個哈希函數，并插入n個元素，自然就可以得到該比特仍然為0的概率是：

 

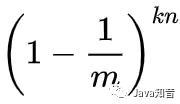
反過來講，它已經被置為1的概率就是：

 

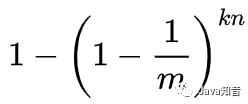
也就是說，如果在插入n個元素后，我們用一個不在集合中的元素來檢測，那么被誤報為存在于集合中的概率（也就是所有哈希函數對應的比特都為1的概率）為：

 

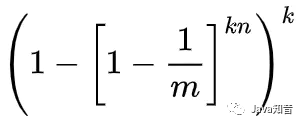
當n比較大時，在查詢了相關資料之后，可以近似得出誤判率的公式大致如下：（本人數學不是太好，這段公式是請教其他大佬得出的）

 

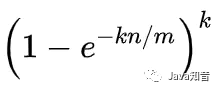
所以，在哈希函數的個數k一定的情況下：

• 位數組長度m越大，誤判率越低；
• 已插入元素的個數n越大，誤判率越高。

盡管說布隆過濾器在使用的時候會有誤判的情況發生，但是在對于數據的準確性有一定容忍度的情況下，使用布隆過濾器還是會比較推薦的。

在實際的項目應用中，布隆過濾器經常會被用在一些大規模去重，但又允許有小概率誤差的場景中，例如說我們對一組爬蟲網頁地址的去重操作，或者統計某些大型網站每天的用戶訪問數量（需要對相同用戶的多次訪問進行去重）。

實際上，關于bitmap和布隆過濾器這類工具在大型互聯網企業上已經受到了廣泛使用，例如說java里面提供了BitSet類，Redis也提供了相應的位圖類，Google里面的guava工具包中的BloomFilter也已經實現類布隆過濾器，所以在實際應用的時候只需要直接使用這些現有的組件即可，避免重復造輪子的情況發生。 

4.Redis提供的BitMap

在redis里有一個叫做bitmap的數據結構，使用技巧如下： 

setbit指令

語法：setbit key offset value
127.0.0.1:6379> setbit bitmap-01 999 0
(integer) 0
127.0.0.1:6379> setbit bitmap-01 999 1
(integer) 0
127.0.0.1:6379> setbit bitmap-01 1003 1
(integer) 0
127.0.0.1:6379> setbit bitmap-01 1003 0
(integer) 1
127.0.0.1:6379> setbit bitmap-01 1004 0
(integer) 0 

注意：

1.offset 參數必須大于或等于 0 ，小于 2^32 (bit 映射被限制在 512 MB 之內)。

2.因為 Redis 字符串的大小被限制在 512 兆(megabytes)以內， 所以用戶能夠使用的最大偏移量為 2^29-1(536870911) ， 如果你需要使用比這更大的空間， 請使用多個 key。

3.當生成一個很長的字符串時， Redis 需要分配內存空間， 該操作有時候可能會造成服務器阻塞(block)。在2010年出產的Macbook Pro上， 設置偏移量為 536870911(512MB 內存分配)將耗費約 300 毫秒， 設置偏移量為 134217728(128MB 內存分配)將耗費約 80 毫秒， 設置偏移量 33554432(32MB 內存分配)將耗費約 30 毫秒， 設置偏移量為 8388608(8MB 內存分配)將耗費約 8 毫秒。 

getbit指令

語法：getbit key offset

返回值：

127.0.0.1:6379> setbit bm 0 1
(integer) 0
127.0.0.1:6379> getbit bm 0
(integer) 1  
  

bitcount指令

語法：bitcount key [start] [end]  ，這里的start和end值為可選項

返回值：被設置為 1 的位的數量

127.0.0.1:6379> bitcount user18 
(integer) 4  
  

bitop指令

語法：bitop operation destkey key [key ...]

operation 可以是 AND 、 OR 、 NOT 、 XOR 這四種操作中的任意一種：

BITOP AND destkey key [key ...] ，對一個或多個 key 求邏輯并，并將結果保存到 destkey 。
BITOP OR destkey key [key ...] ，對一個或多個 key 求邏輯或，并將結果保存到 destkey 。
BITOP XOR destkey key [key ...] ，對一個或多個 key 求邏輯異或，并將結果保存到 destkey 。
BITOP NOT destkey key ，對給定 key 求邏輯非，并將結果保存到 destkey 。  
  

實戰案例

統計某個用戶在xx論壇的簽到次數，這里假設用戶的id為u18

127.0.0.1:6379> setbit user18 1 1
(integer) 0
127.0.0.1:6379> setbit user18 2 1
(integer) 0
127.0.0.1:6379> setbit user18 5 1
(integer) 0
127.0.0.1:6379> setbit user18 15 1
(integer) 0
127.0.0.1:6379> bitcount user18 
(integer) 4 

通過使用bitcount指令可以快速從redis中計算出user18的簽到天數。

( ps:但是如果要計算出連續簽到的天數，或者記錄更多的簽到信息，并且考慮上數據存儲的可靠穩定性，那么此時bitmap就不太適用了，這里我只是模擬了一個案例供大家學習這條指令的使用。) 

按天統計網站活躍用戶

設計思路，用天來作為統計的key，然后以用戶ID作為Offset，一旦用戶登錄訪問網站，則根據其用戶id計算出對應的offset并且將其設置為1。

//2020年10月21日 用戶11034訪問網站
127.0.0.1:6379> setbit 20201021 11034 1
(integer) 0
//2020年10月21日 用戶11089訪問網站
127.0.0.1:6379> setbit 20201021 11089 1
(integer) 0
//2020年10月21日 用戶11034訪問網站
127.0.0.1:6379> setbit 20201022 11034 1
(integer) 0
//2020年10月21日 用戶11032訪問網站
127.0.0.1:6379> setbit 20201023 11032 1
(integer) 0
//通過使用bitop or 做多個集合的交集運算，計算出2020年10月21日 至2020年10月22日
//內連續登錄的用戶id，并且將其放入到名為active_user的bitmap中
127.0.0.1:6379> bitop or active_user 20201021 20201022
(integer) 1387
//提取活躍用戶信息
127.0.0.1:6379> bitcount active_user
(integer) 2
127.0.0.1:6379>  
  

用戶在線狀態、在線人數統計

//模擬用戶98321訪問系統
127.0.0.1:6379> setbit online_member 98321 1
(integer) 0
127.0.0.1:6379> setbit online_member 13284 1
(integer) 0
127.0.0.1:6379> setbit online_member 834521 1
(integer) 0
127.0.0.1:6379> bitcount online_member
(integer) 3
//模擬用戶13284離開系統，在線人數減1
127.0.0.1:6379> setbit online_member 13284 0
(integer) 1
127.0.0.1:6379> bitcount online_member
(integer) 2
127.0.0.1:6379> 

這段指令案例將會員id作為來offset位置，存入到來bitmap中，通過設置相應到bitmap，當有對應會員登錄訪問的時候，對應offset位置則置為1，最后通過bitcount來統計該bitmap中有多少個項為1，從而計算出用戶在線的人數。 

Guava提供的布隆過濾器

對應的依賴：

<dependency>
    <groupId>com.google.guava</groupId>
    <artifactId>guava</artifactId>
    <version>22.0</version>
</dependency>

引入相關的依賴之后，可以通過編寫一個簡單的案例來理解guava里面提供的布隆過濾器組件：

packageorg.idea.guava.filter;
import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnels;
/**
* @author idea
* @date created in 11:05 上午 2020/10/25
*/
public class GuavaBloomFilter {
public static void main(String[] args) {
//創建布隆過濾器時要傳入期望處理的元素數量，及最期望的誤報的概率。
    BloomFilter<Integer> bloomFilter = BloomFilter.create(
Funnels.integerFunnel(),
100,  //希望存儲的元素個數
0.01  //希望誤報的概率
);
bloomFilter.put(1);
bloomFilter.put(2);
bloomFilter.put(3);
bloomFilter.put(4);
bloomFilter.put(5);
        //判斷過濾器內部是否存在對應的元素
System.out.println(bloomFilter.mightContain(1));
System.out.println(bloomFilter.mightContain(2));
System.out.println(bloomFilter.mightContain(1000));
}
} 

這段代碼中你可能會疑惑，為什么是mightContain而不是contain呢？

這一點其實和布隆過濾器本身的誤判機制有關。

布隆過濾器常用的場景為：

對于一些緩存穿透的場景可以用于做為預防手段。

本身的優點：

存儲空間消耗較少。

時間效率高，查詢和插入的時間復雜度均為O(h)。（h為hash函數的個數）

缺點：

查詢元素是否存在的概率不能保證100%準確，會有部分誤判的情況存在。

只能插入和查詢元素，不允許進行刪除操作。