您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
樸素貝葉斯分類器是基于貝葉斯理論中屬性獨立假設而創造的一種算法。算法思路簡單:只要是哪個類的后驗概率大待測樣本即為該類別。所謂后驗概率就是在給定條件發生的情況下,該樣本被判定為某個類別的概率。后驗概率P(Y|X)表示在屬性集合X(X1,X2,...,Xn)發生的條件下Y類別發生的概率,所以只要計算這個概率就行了,問題的關鍵在于這個概率該怎么求?
下面貝葉斯告訴了我們一種方法來求這個概率:
P(Y|X) = P(X|Y)P(Y)/P(X),我們稱P(X|Y)為類條件概率密度,P(Y)為先驗概率。假設待測分類問題是個二分問題兩個類別分別為Y1、Y2。所以我們要做的就是求出P(Y1|X)和P(Y2|X)的大小,如果P(Y1|X)>P(Y2|X)則樣本被判為類別Y1,反之亦然。從上面的分析中我們知道P(Y|X)可以利用貝葉斯公式進行轉化,而且對于不同的類分母P(X)都是相同的,即只需要比較P(X|Y)P(Y)大小就可以了。
現在我們需要求兩個值:1、P(X|Y) 2、P(Y)
P(X|Y)的求解依賴一個假設,即假設屬性之間條件獨立。用公式表示為:P(X|Y1) =∏P(Xi|Y=Y1) (i = 1,2,...,n)。
P(Y),可以用數據表中的數據直接得到。
舉個列子:

有了上面這些表格我們就可以很方便的計算某個待測樣本的后驗概率了,比如給定一個樣本X = (有房=否,婚姻狀況=已婚,年收入=120),判定該樣本屬于哪個類?
有上面的分析我們只需計算兩個概率P(No|X)和P(Yes|X):
P(No|X)= P(有房=No) * P(婚姻=已婚|No)* P(年收入=120) = 4/7 * 4/7 * 0.0072 = 0.0024
P (Yes|X) = P(有房=Yes) * P(婚姻=已婚|Yes)* P(年收入=120) = 1 * 0 * 1.2*10e(-9) = 0
因為P(No|X) > P (Yes|X),所以判定樣本屬于類No。
但是上述計算過程中有兩個問題:
1、對于零次出現的屬性它的概率怎么處理,因為如果這個屬性集合如(婚姻=已婚|Yes)沒有出現所以導致任何出現包含該集合的屬性集的后驗概率一律為零,顯然這是不合理的。
2、對于屬性集中的連續屬性如何求它的概率(如上面的年收入)?
對第一個問題我們采用拉普拉斯平滑(也稱加一平滑)方法,也即對每個屬性組合的頻數都加一之后再求他的概率,如下所示
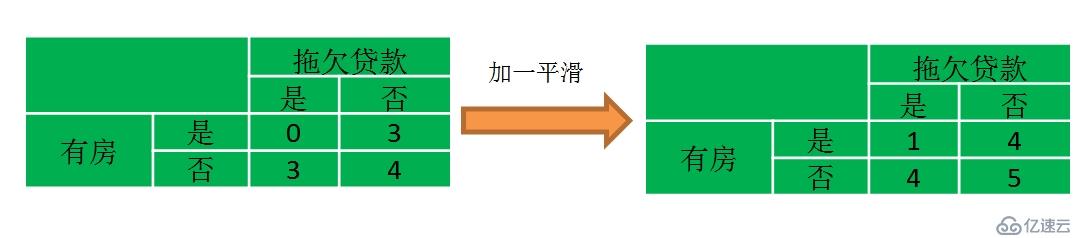
對第二個問題我們可以用分布估計的方法來處理,如上對于年收入屬性我們可以假設它符合高斯分布,我么可以用如下的公式估計參數:
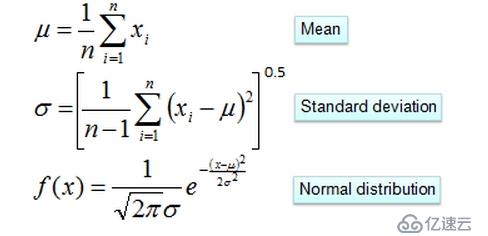
得到最后一個公式之后就可以計算相應給定樣本的概率了。
樸素貝葉斯分類器的特點:
1、抗干擾能力強,對鼓勵的噪聲點健壯,因為它在求概率的過程中將噪聲平均化;
2、面對無關屬性,分類器健壯,因為類條件概率不會對后驗概率計算產生影響;
3、相關屬性會降低分類器性能,因為條件獨立假設此時不成
需要總結的大概就是這么多,歡迎批評指正!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。