您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
LDA也稱Fisher線性判別法,它是一種非迭代的分類算法。算法的主要思想將特征空間中的樣本投影到該空間的一條直線上以實現從高維到一維的數據壓縮。顯然這樣的投影有很多方向,而LDA算法就是尋找一個最佳投影方向來使樣本的類內距離最小而類間距離最大。
投影方向:1、投影后不同類別的樣本均值的差別應盡可能大,即類間距離盡可能大;2、投影后相同類別的樣本方差應盡可能小,即類內距離應盡可能小。
定義一個Fisher準則函數(關于準則函數是如何確定的可以參看相關課本),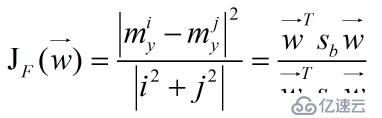
其中向量W是投影的方向向量,Sb和Sw是投影前兩類別的類間和類內離散度矩陣。這樣求投影方向的問題就轉化為求該準則函數最大值的問題。我們可以采用Lagrange乘子法求解該函數的極值,令函數的分母為常數C作為求解的一個約束條件(因為對任意的實數a,均有J(aw)=J(w))。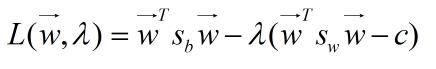
然后就是Lagrange對求導,最后得到最佳的投影方向為:

如果對Lagrange乘子法不是很了解參見:http://www.cnblogs.com/zhangchaoyang/articles/2726873.html
算法步驟:
輸入訓練樣本集;
計算兩個類別的均值向量;
計算類內總的離散度矩陣;
計算類內總離散度矩陣的逆陣;
獲得投影方向,公式如上。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。