您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了C語言字符串和數組怎么定義使用的相關知識,內容詳細易懂,操作簡單快捷,具有一定借鑒價值,相信大家閱讀完這篇C語言字符串和數組怎么定義使用文章都會有所收獲,下面我們一起來看看吧。
字符串簡稱串,是一種特殊的線性表,其特殊性在于數據元素僅由一個個字符組成。作為一種基本數據類型,字符在計算機信息處理中意義非同一般,計算機非數值處理的對象經常是字符串數據。另外,串還具有自身的特性,常常把一個串作為一個整體來處理,因此,把串作為獨立結構的概念加以研究是非常有必要的。本章簡單介紹了串的存儲結構及基本運算。
數組可視為線性表的推廣,其特點是表中數據元素仍然是一個表。從本質上看,維數大于1的數組中數據元素之間不再是簡單的一對一關系,因此,嚴格地說多維數組是非線性的。然而,由于數組中數據元素類型的一致性和其內部結構上的同一性,在實際處理數組時可以借助線性表的方法來實現數組及其運算。本章將會介紹數組的邏輯結構和存儲結構、稀疏矩陣及其壓縮存儲等內容。
1.1 串的基本概念
串(String)是由零個或多個任意字符串組成的字符序列。記做:s ="a1a2··an",其中,s是串名。a1(1<=i <=n)是一個任意字符,i是該元素在整個串中的序號;n為串的長度,表示串中所包含的字符個數,當n=0時,稱為空串。
子串和主串:串中任意連續的字符組成的子序列稱為該串的子串;包含子串的串相應地稱為主串。
子串的位置:子串的第一個字符在主串中的序號稱為子串在主串中的位置。
串相等:若兩個串的長度相等且每一個對應字符都相等,就稱這兩個串是相等的。
1.2 串的基本運算
求串長:StrLength(s);
串賦值:StrAssign(s1,s2); // 將s2的串值賦予s1
連接運算:StrConcat(s1,s2,s) 或 StrConcat(s1,s2).//在s1后面連接s2的串值,產生新串s
求子串:SubStr(s,i,len);//返回s的第i至len個字符的子串值。len=0為空串。例如:SubStr("abcdefg",2,3) = "bcd"
串比較:StrComp(s1,s2);//若s1 =s2 ,操作返回值為0;s1<s2,返回值<0;反之>0
串定位:StrIndex(s,t);//若t被包含于s中,則返回值為t的位置,反之值為-1
串插入:StrInsert(s,i,t);//將串t插入到s的第i個字符位置上
串刪除:StrDelete(s,i,len);//刪除串t中第i至len個字符的子串
串修改:StrRep(s,t,r);//用串r替換s中出現的所有與串t相等且不重疊的子串
1.3 串的存儲結構
因為串是數據元素類型為字符的線性表,所有線性表的存儲方式仍適用于串,也因為字符的特殊性和字符串經常作為一個整體來處理的特點,串在存儲時還有一些與一般線性表不同的地方。
1、串的定長順序存儲結構:
類似于順序表,可以用一組地址連續的存儲單元存儲串值中的字符串序列,所謂定長是指按預定義的大小為每一個串變量分配固定長度的存儲區。如下,串的最大長度不能超過256。
#define MAXSIZE 256 char s[MAXSIZE]
標識實際長度的常用方法有三種:
第一種:類似順序表,用一個指針來指向最后一個字符,這樣表示的串描述如下:
typedef struct{
char data[MAXSIZE];
int curlen;
}SeqString;
SeqString s;//串變量這種存儲方式可以直接得到串的長度:s.curlen+1 。
第二種:在串尾存儲一個不會在串中出現的特殊字符串作為串的終結符,以此表示串的結尾。例如,C語言中處理定長串的方法就是這一點,它用“\0”來表示串的結束。這種存儲方法不能直接得到串的長度,根據當前字符是否是“\0”來確定串是否結束,從而計算出串的長度。
第三種:設定串長存儲空間:chars[MAXSIZE+1],用s[0]來存放串實際長度,而串值存放在s[1]~s[MAXSIZE]中,字符的序號和存儲位置一致,應用更為方便。
2、堆分配存儲結構
在順序串上的插入、刪除操作并不方便,必須移動大量的字符,而且當操作中出現串值序列的長度超過上界MAXSIZE時,只能用截尾法處理。要克服這個弊病,只有不限定串的最大長度,動態分配串值的存儲空間。
堆分配存儲結構的特點是:仍以一組地址連續的存儲單元存放串的字符序列,但其存儲空間是在算法執行過程中動態分配得到的。在C語言中,由動態分配函數malloc()和free()來管理。利用函數malloc()為每一個新產生的串分配一塊實際需要的存儲空間,若分配成功,則返回一個指針,指向串的起始地址。串的對分配存儲結構如下:
typedef struct{
char *ch;
int len;
}HSTRING:由于堆分配存儲結構的串既有順序存儲結構的特點,在操作中又沒有串長的限制,顯得很靈活,因此,在串處理的應用程序中常被選用。
3、定長順序串基本運算的實現
串連接:把兩個串s1和s2首尾連接成一個新串s,即s<-s1+s2
int StrConcat(s1,s2,s)
char s1[],s2[],s[];//將串s1,s2合并到串s,合并成功返回1,否則返回0
{
int i =0,j,len1,len2;
len1 = StrLength(s1);
len2 = StrLength(s2);
if(len1+len2>MAXSIZE-1) return 0; //s 長度不夠
j = 0 ;
while(s1[j]! ="\0"){
s[i] = s1[j];
i++;
j++;
}
while(s2[j]! ="\0"){
s[i] = s2[j];
i++;
j++;
}
s[i] = "\0";
return 1;
}求子串:
int StrSub(char *t ,char *s,int i , in len){
//用t返回串s中第i個字符串開始的長度為len的子串,1<=i串長
int slen;
slen = StrLength(s);
if(i<1 || i>slen || len<0 || len>slen-i+1){
return 0;
}
for(j =0 ; j<len ; j++){
t[j] =s[i+j-1];
t[j] ="\0";
return 1;
}
}串比較:
int StrComp(char *s1 ,char *s2){
int i =0;
while(s1[i] == s2[i] && s1[i]!="\0"){
i++;
}
return (s1[i] -s2[i]);
}串定位:
int StrIndex(char *s ,char *t)
//返回子串t在主串s中的位置,若不存在則返回-1
{
int i=0, j = 0;
while(s[i] !="\0" && t[j] !="\0"){
if(s[i] == t[j]){//匹配成功,繼續比較下一個字符
++i;
++j;
}else{ //否則主串換一個起始位置,子串重0開始
i = i-j+1;
j =0;
}
if( t[j] == "\0") { //匹配成功,返回匹配的第一個字符位置
return i -j;
}else{
return -1;
}
}子串的定位操作通常稱做串的模式匹配,是各種串處理系統中最重要的操作之一。上面的算法是一種簡單的帶回溯的匹配算法,該算法思路比較簡單,容易理解,但其視覺復雜度較高,最壞情況下為O(slen*slen)。
2.1 數組的邏輯結構和基本操作
數組(Array)是一種數據結構,高級語言一般都支持數組這種數據類型。特點是結構中的元素本身可以是具有某種結構的數據,但屬于同一數據類型。從邏輯結構上,可以把數組看做一般線性表的擴充。例如,一維數組就是一個線性表,二維數組就是"數據元素是一維數組"的一維數組。以此類推,即可得到多維數組的定義。
如有一個m行n列的二維數組:
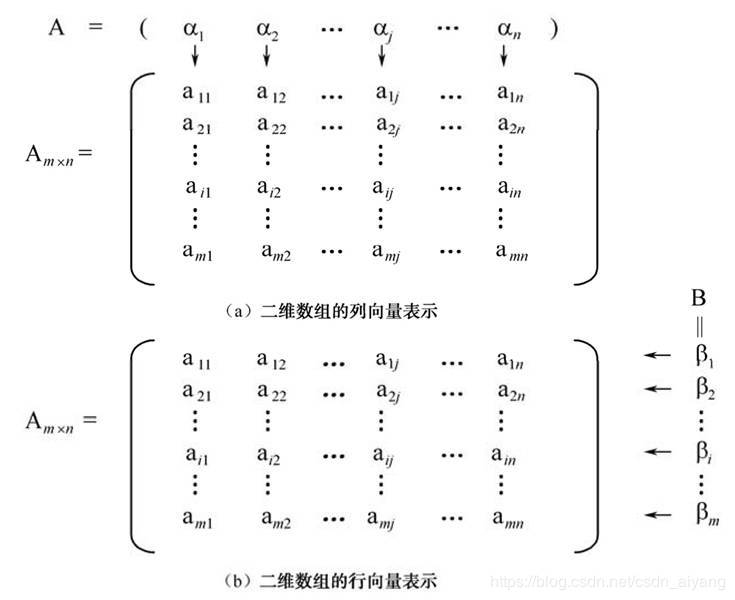
可以把二維數組看成是一個線性表:A=(a1,a2····,an),其中aj(1<=j<=n)本身也是一個線性表,稱為列向量(Column Vector),即aj=(a1j,a2j···,amj)。同樣還可以將數組A看成另外一個線性表:B={B1,B2,···,Bm),其中Bi(1<=i<=n)本身也是一個線性表,稱為行向量(Row Vector),即Bi=(ai1,ai2,····aim)。
在二維數組中,元素aij處在第i行和第j列的交叉處,即元素aij同時有兩個線性關系約束,aij既是同行元素aij-1 的“行后繼”,又是同列元素ai-1j的“列后繼”,又是同列元素ai-1j的“列后繼”。同理,三維數組可以看成這樣的一個線性表,即其中每個數據元素均是一個二維數組,即三維數組中每個元素同時有三個線性關系約束,推廣之,n維數組就是“數據元素為n-1維數組”的線性表。
由數組的結果可以看出,數組中的每一個元素由一個值和一組下表來描述。值表示數組中元素的數據信息,下標用來描述該元素咋數組中的相對位置。數組的維數不同,描述其相對位置的下標的個數也不同。例如,在二維數組中,元素aij由兩個下標i、j來描述,其中i表示該元素的行號,j表示該元素的列號。
數組是一個具有固定格式和數量的數據有序集,即,一旦定義了數組的維數和每維的上、下限,數組的元素個數就固定了,而且數組中的每一個元素也由唯一的一組下標來標識。因此,在數組上一般不能做插入、刪除數據元素的操作。對數組的操作通常只有下面兩類。
(1)取值操作:給定一組下標,讀其對應的數據元素。
(2)賦值操作:給定一組下標,存儲或修改與其相對應的數據元素。
因此,數組的操作注意是數據元素的定位,即給定元素的下標,得到該元素在計算機中的存儲位置。其本質就是地址計算問題。接下來以二維數組展開說明,因為二維數組是應用最廣泛的,也是最基本的,對于大于二維的多維數組的存儲和操作方法可以類推。
2.2 數組的存儲結構
由于數組的特點是數組中數據元素的個數固定且其結構不變化,數組操作基本就是取值、賦值運算,因此,對于數組而言,采用順序存儲結構表示比較合適。對于一維數組可以直接按其下標順序分配內存空間;而對于多維數組,必須按某種次序將數組中元素排成一個線性序列,然后按該序列將數據元素存放在一維的內存空間中。
存儲二維數組時,一般有兩種存儲方式:第一種是以行序為主序(先行后列)的順序存儲方式,即從第一行開始存放,一行存放完了接著存放下一行,直到最后一行為止;另一種是以列序為主序(先列后行)的順序存儲方式,即一列一列的存儲。
以行序為主序的存儲分配的規律是:最右邊的下標先變化,即最右下標從小到大,循環一遍后,右邊第二個下標再變,···,從右向左,最后是左下標。以列序為主序存儲分配的規律恰好相反:最左邊的下標先變化,即最左下標從小到大,循環一遍后,左邊第二個下標再變,···,從左向右,最后是右下標。例如,一個2X3的二維數組,以行序為主序的分配順序為:a1,a2,a3 | a4,a5,a6 ;以列序為主序的分配順序為:a1,a4 | a2 ,a5| a3,a6 。
設有m × n 二維數組Amn ,按元素的下標求存儲地址:
以行序為主序為例:設數組的基址為LOC(a11),每個數組元素占據L個地址單元,那么aij的物理地址可用一線性尋址函數計算:LOC(aij) = LOC(a11)+((i-1)× n+j-1) ×L 。因為數組元素aij的前面有i-1行,每一行的元素個數為n,在第i行中它的前面還有j-1個數組元素。在C語言中,數組中每一維的下屆定義為0,則:LOC(aij) = LOC(a00) +(i×n+j)×L。
推廣到一般二維數組A[c1···d1][c2···d2],則aij的物理地址計算函數為:LOC(aij) = LOC(ac1c2) +((i-c1) ×(d2-c2+1)+(j-c2))×L。同理,對于三維數組Amnp,即m×n×p數組,數組元素aijk的物理地址為:LOC(aijk) = LOC(a111)+((i-1)×n×p+(j-1)×p+k-1)×L。
2.3 稀疏矩陣
稀疏矩陣(Sparse Matrix)是指矩陣中大多數元素為零元素的矩陣,即設m×n矩陣中有t個非零元素且t<<m×n ,則稱之為稀疏矩陣。
很多科學管理及工程計算中,常會遇到階數很高的大型稀疏矩陣。如果按常規分配方法,順序分配在計算機內,那將是相當浪費內存的。為此提出另外一種存儲方法,僅存放非零元素。但對于這類矩陣,通常零元素分布沒有規律,為了能找到相應的元素,僅存儲非零元素的值是不夠的,還要記下它所在的行和列。于是采取如下方法:非零元素所在的行、列及它的值構成一個三元組(i,j,v),然后按某種規律存儲這些三元組,這種方法可以大大節約存儲空間。
1、稀疏矩陣的三元組表存儲
將三元組按行優先的順序,同一行中列號從小到大的規律排列成一個線性表,稱為三元組表,采用順序存儲方法存儲該表。如下圖:
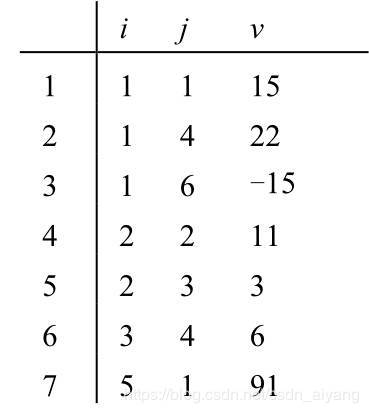
這種存儲結構的具體實現如下:
#define SMAX 1024 //足夠大的空間
typedef struct{
int i ,j ; //非零元素的行、列
datatype v; //非零元素值
}SPNode; //三元組類型
typedef struct{
int mu,nu,tu; //行列及非零元素個數
SPNode data[SMAX];//三元組表
}SPMatrix; //三元組表的存儲類型
//定義一個稀疏矩陣的變量:
SPMatrix M;稀疏矩陣的轉置運算:
設A為一個m×n的稀疏矩陣,則其轉置矩陣B就是一個n×m的稀疏矩陣,因此它們可以采用相同的數據類型,即:
SPMatrix A,B;
轉置運算需要完成的工作包括:A的行、列分別轉化成B的列、行;將A.data中每一個三元組的行與列交換后復制到B.data中。以上兩點完成之后,似乎完成了B,但實際上沒有。因為前面規定的三元組表是按行從小到大且同一行中的元素按列號從小到大的規律順序存放的,因此轉置后的矩陣B也必須按此規律排列。算法思路如下:
(1)A的行、列轉行成B的列、行;
(2)在A.data中依次找第一列的、第二列的直到最后一列的三元組,并將找到的每個三元組的行、列交換后順序存儲到B.data中即可。
void TransM1(SPMatrix *A){
SPMatrix *B;
int p,q,col;
B = malloc(sizeof(SPMatrix));//申請存儲空間
B ->mu =A ->nu;
B ->nu =A ->mu;
B ->tu =A ->tu;//稀疏矩陣的行、列、元素個數
if(B->tu>0){
q=0;
for(col =1 ;col <=(A->nu);col++){//掃描整個三元組數
for(p=1;p<(A->nu);col++){
if(A->data[p].j == col){
B->data[q].i = A ->data[p].j;
B->data[q].j = A ->data[p].i;
B->data[q].v = A ->data[p].v;
q++;
}
}
}
}
if(B->tu > 0){
return B;
}
}分析該算法,其時間主要耗費在col和p的二重循環上,所以時間復雜性為O(n×t)(設m、n是原矩陣的行、列數,他是稀疏矩陣的非零元素個數),顯然,當非零元素的個數t和m×n同數量級時,算法的時間復雜度為O(m×n2),和通常存儲方式下矩陣轉置算法相比,可能節約了一定量的存儲空間,但算法的時間復雜度更差了一些。
算法改進:上面算法低效率的原因是算法要從A的三元組表中尋找第一列、第二列、···,要反復查找A,若能直接確定A中每一三元組在B中的位置,則對A的三元組表掃描一次即可。這是可以做到的,因為A中第一列的第一個非零元素一定存儲在B.data[1]中,如果還知道第一列的非零元素的個數,那么第二列的第一個非零元素在B.data中的位置便等于第一列的第一個非零元素在B.data中位置加上第一列的非零元素的個數。以此類推,因為A中三元組的存放順序是先行后列,對同一行來說,必定先遇到列號小的元素,這樣只需掃描一遍A.data即可。
根據上面的想法,需要引入兩個向量來實現:num[n+1]和cpot[n+1],num[col]表示矩陣A中第col列的非零元素的個數(為了方便均從1單元用起),cpot[col]初始值表示矩陣A中的第col列的第一個非零元素在B.data中位置。于是cpot的初始值為:cpot[1] =1 ;cpot[col] = cpot[col-1]+num[col -1]; 2<=col<=n 。
SPMatrix *TransM2(SPMatrix *A){
SPMatrix *B;
int i,j,l;
int num[n+1],cpot[n+1];
B = malloc(sizeof(SPMatrix));//申請空間
//稀疏矩陣行列元素個數
B->mu = A ->nu;
B->nu =A ->mu;
B ->tu =A ->tu;
if(B->to > 0){
for(i=1;i<=A->nu;i++){
num[i] = 0;
}
for(i=1 ;i<=A ->tu ;i++){
j=A->data[i].j;
num[j]++;
}
cpot[1] =1; //求矩陣A中每一列第一個非零元素在B.data中的位置
for(i =2 ;i<A->nu;i++){
cpot[i] =cpot[i-1]+num[i-1];
}
for(i =1 ;i<(A->tu);i++){ // 掃描三元組表
j =A->data[i].j;
k =cpot[j];
B->data[k].i = A->data[i].j;
B->data[k].j = A ->data[i].i;
B->data[k].v = A->data[i].v;
}
return B;
}分析這個算法的時間復雜度:這個算法中有四個循環,分別執行了n、t、n-1、t次,在每一個循環中,每次迭代的實際是一個常量,因此總的時間復雜度是O(n+t)。當然,它所需要的存儲空間比前一個算法多了兩個向量的存儲空間。
關于“C語言字符串和數組怎么定義使用”這篇文章的內容就介紹到這里,感謝各位的閱讀!相信大家對“C語言字符串和數組怎么定義使用”知識都有一定的了解,大家如果還想學習更多知識,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。