如何分析基于SVM及瀏覽器特性的數據防偽造技術

這期內容當中小編將會給大家帶來有關如何分析基于SVM及瀏覽器特性的數據防偽造技術，文章內容豐富且以專業的角度為大家分析和敘述，閱讀完這篇文章希望大家可以有所收獲。

前言

    在安全攻防領域，攻擊者常常會通過偽造瀏覽器信息（例如：userAgent、cookie等等）來模擬正常業務請求，達到自動化模擬重復請求的效果，進而制造暴力訪問，信息遍歷，羊毛擼取。這樣的數據偽造方式影響惡劣，而且識別困難。下面就介紹一種瀏覽器基因技術集合機器學習算法來智能識別數據偽造的有效做法。

支持向量機(SupportVector Machine，SVM)

   支持向量機即SVM法(Support Vector Machine)，由Vapnik等人于1995年提出，具有相對優良的性能指標。該方法是建立在統計學習理論基礎上的機器學習方法。通過學習算法，SVM可以自動尋找出那些對分類有較好區分能力的支持向量，由此構造出的分類器可以最大化類與類的間隔，因而有較好的適應能力和較高的分準率。該方法只需要由各類域的邊界樣本的類別來決定最后的分類結果。支持向量機算法的目的在于尋找一個超平面H(d),該超平面可以將訓練集中的數據分開，且與類域邊界的沿垂直于該超平面方向的距離最大，故SVM法亦被稱為最大邊緣(maximum margin)算法。待分樣本集中的大部分樣本不是支持向量，移去或者減少這些樣本對分類結果沒有影響，SVM法對小樣本情況下的自動分類有著較好的分類結果。

  SVM方法是通過一個非線性映射p，把樣本空間映射到一個高維乃至無窮維的特征空間中（Hilbert空間），使得在原來的樣本空間中非線性可分的問題轉化為在特征空間中的線性可分的問題。簡單地說，就是升維和線性化。升維，就是把樣本向高維空間做映射，一般情況下這會增加計算的復雜性，甚至會引起“維數災難”，因而人們很少問津。但是作為分類、回歸等問題來說，很可能在低維樣本空間無法線性處理的樣本集，在高維特征空間中卻可以通過一個線性超平面實現線性劃分（或回歸）。一般的升維都會帶來計算的復雜化，SVM方法巧妙地解決了這個難題：應用核函數的展開定理，就不需要知道非線性映射的顯式表達式；由于是在高維特征空間中建立線性學習機，所以與線性模型相比，不但幾乎不增加計算的復雜性，而且在某種程度上避免了“維數災難”。這一切要歸功于核函數的展開和計算理論。

  SVM里面最重要的兩個點就是核函數及求解算法SequentialMinimal Optimization（簡稱SMO）。

核函數

   1、方法原理

    根據模式識別理論，低維空間線性不可分的模式通過非線性映射到高維特征空間則可能實現線性可分，但是如果直接采用這種技術在高維空間進行分類或回歸，則存在確定非線性映射函數的形式和參數、特征空間維數等問題，而最大的障礙則是在高維特征空間運算時存在的“維數災難”。采用核函數技術可以有效地解決這樣問題。

    設x,z∈X,X屬于R（n）空間,非線性函數Φ實現輸入間X到特征空間F的映射,其中F屬于R（m）,n<<m。根據核函數技術有：

      K(x,z) =<Φ(x),Φ(z) >               

    其中：<, >為內積,K(x,z)為核函數。從上式可以看出，核函數將m維高維空間的內積運算轉化為n維低維輸入空間的核函數計算，從而巧妙地解決了在高維特征空間中計算的“維數災難”等問題，從而為在高維特征空間解決復雜的分類或回歸問題奠定了理論基礎。

  2、特點

    核函數方法的廣泛應用,與其特點是分不開的：

    1）核函數的引入避免了“維數災難”,大大減小了計算量。而輸入空間的維數n對核函數矩陣無影響，因此，核函數方法可以有效處理高維輸入。

    2）無需知道非線性變換函數Φ的形式和參數.

    3）核函數的形式和參數的變化會隱式地改變從輸入空間到特征空間的映射，進而對特征空間的性質產生影響，最終改變各種核函數方法的性能。

    4）核函數方法可以和不同的算法相結合，形成多種不同的基于核函數技術的方法，且這兩部分的設計可以單獨進行，并可以為不同的應用選擇不同的核函數和算法。

3、常見的核函數

     多項式核：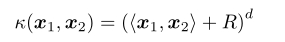

      高斯核（徑向基函數）：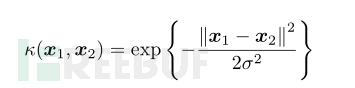

       徑向基函數（Radical Basis Function，RBF）。徑向基函數（Radical Basis Function，RBF）方法是Powell在1985年提出的。所謂徑向基函數，其實就是某種沿徑向對稱的標量函數。通常定義為空間中任一點x1到某一中心x2之間歐氏距離的單調函數，可記作k(||x1-x2||)，其作用往往是局部的，即當x1遠離x2時函數取值很小。

       線性核：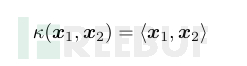

       即是兩個矩陣空間的內積。

SMO算法過程

   SMO的主要兩個步驟就是：

    1、選擇需要更新的一對α-i和α-j采取啟發式的方式進行選擇，以使目標函數最大程度的接近其全局最優值；

     2、將目標函數對α-i和α-j進行優化，以保持其它所有α不變。 所需要的約束條件為：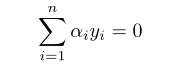

核心算法實現

      1、核函數變換，兩種類型實現：線性及高斯核

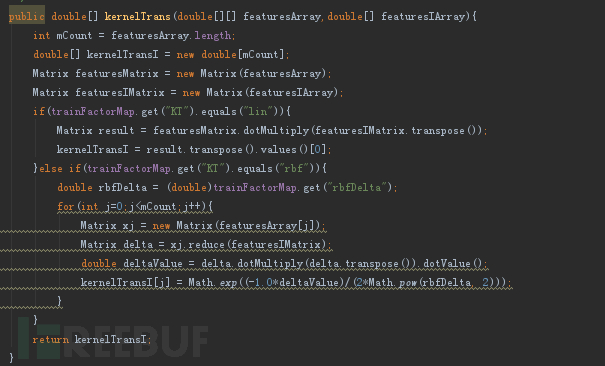
     2、SMO算法實現過程開源都比較多，這里由于篇幅有限不再贅述。

線上特性提取及實現

     瀏覽器特性：

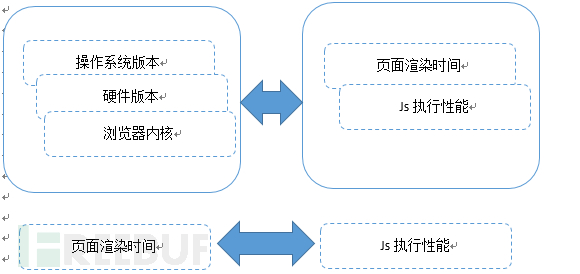
     何謂瀏覽器特性。特性顧名思義就是無法更改，那么瀏覽器特性就是瀏覽器里面那些無法更改的信息。那么什么可以作為瀏覽器的特性呢？我們利用大數據進行分析發現：操作系統版本、硬件版本、瀏覽器內核、頁面渲染時間、js執行性能這些因素單個都可以偽造，但是他們之間的關系很難偽造，我們就嘗試通過這幾個因素之間的關系分析來實現防偽造，如下圖所示：

   線上數據示例：

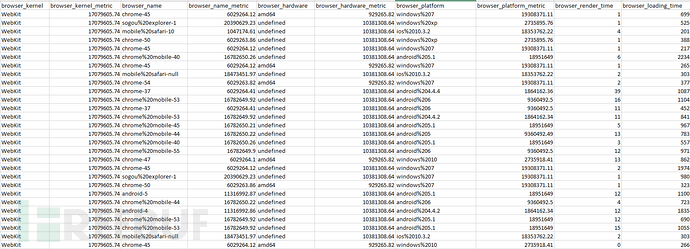
   特性包括有：瀏覽器內核、瀏覽器名稱及版本、運行平臺、運行平臺CPU版本、js執行時間、頁面渲染時間等等，當然還可以擴展，例如瀏覽器的解析dom耗時、白屏耗時、domready耗時等等。而上圖中以metric結尾的是相應特性的hash映射值。

     正負樣本選擇：

       正樣本線上實時采集，負樣本采取隨機打亂組合的方式進行。

模塊算法策略優化

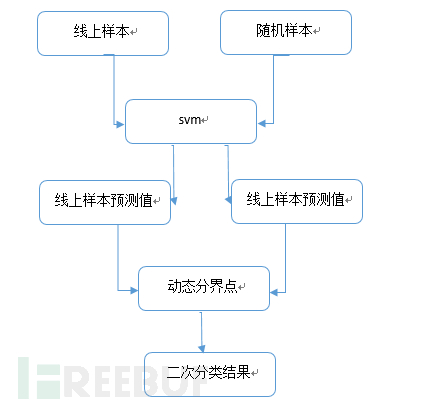
在整個機器學習流程中我們添加了一個動態分界點計算及二次分類的做法，這個做法就是解決分類準確性問題，由于單一固定的分界點事先雖然可以確定，但是分類效果很差，所以我們依據分類后預測的結果值來進行動態選擇，再進行二次分類。這個優化之后將系統的準確性從60%直接升為99%以上，效果顯著。

實驗過程及結果

     我們線上采集10000條數據，并隨機打亂偽造5000數據作為負樣本，通過svm擬合得出一個預測值，并將預測值計算出正負樣本的最大似然分界點，

再依據分界點將預測值進行二次分類。基本流程如下：

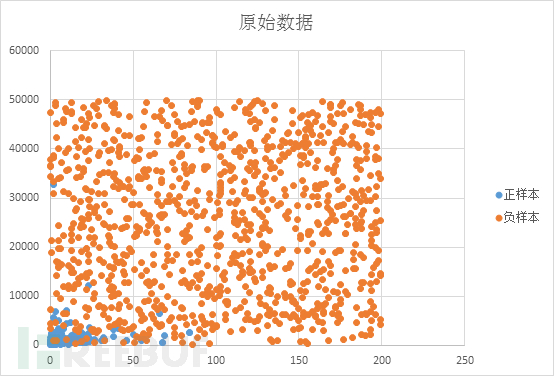
原始數據分布如下圖所示：

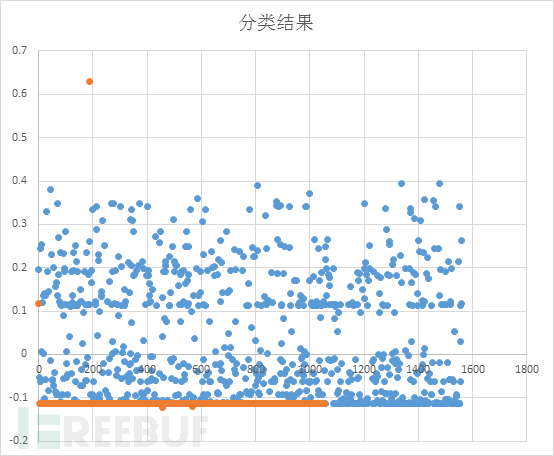
經過算法多次分類之后得到的結果如下：

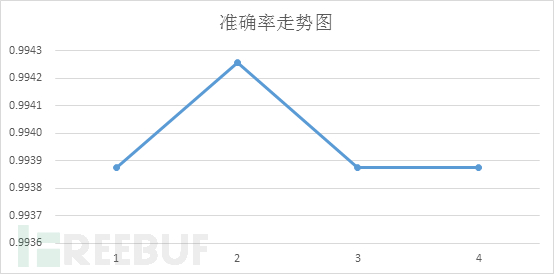
上述就是小編為大家分享的如何分析基于SVM及瀏覽器特性的數據防偽造技術了，如果剛好有類似的疑惑，不妨參照上述分析進行理解。如果想知道更多相關知識，歡迎關注億速云行業資訊頻道。