外排序   敗者樹   多路歸并

一、外排序

排序按數據存在的位置不同分為內排序和外排序

內排序：數據都在內存中，選擇合適的排序方法對數據進行排序，比如選擇排序、快速排序等

              衡量內排序的效率是數據的比較次數

外排序：數據無法全部加載到內存中，只能不斷在外部存儲器和內存中進行交換完成排序

              衡量外排序的效率是內存與外村的交換次數

外排序是針對大文件的數據排序，內存中無法加載這個大文件，把這個文件分為k個小文件，分別排序后合并

http://blog.csdn.net/msdnwolaile/article/details/52084983

二、敗者樹

勝者樹和敗者樹都是完全二叉樹，每個葉子節點相當于一個選手，每個中間節點相當于一場比賽，每一層相當于一輪比賽

勝者樹的中間節點記錄的是勝者的序號，敗者樹的中間節點記錄的是敗者的序號

1、勝者樹

優點是：如果一個選手的數值改變，那么只需沿著一條路徑（這個節點到根節點的路徑）即可修正這顆勝者樹

2、敗者樹

用中間節點記錄敗者，用另一個輔助節點記錄勝者來進行下一場比賽

下面舉一個栗子說明：

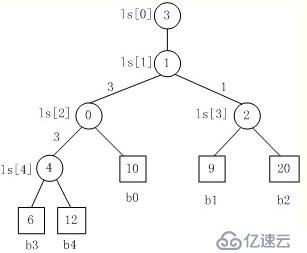
三、K路歸并排序

我們把敗者樹分為兩部分：

第一部分是b[]，用來保存K路數組的首元素，葉節點存放在此處

第二部分式ls[],用來保存敗者數組的下標，b[0]是最終的勝者(即所求的數)，敗者節點存放在此處

1、創建敗者樹

敗者樹

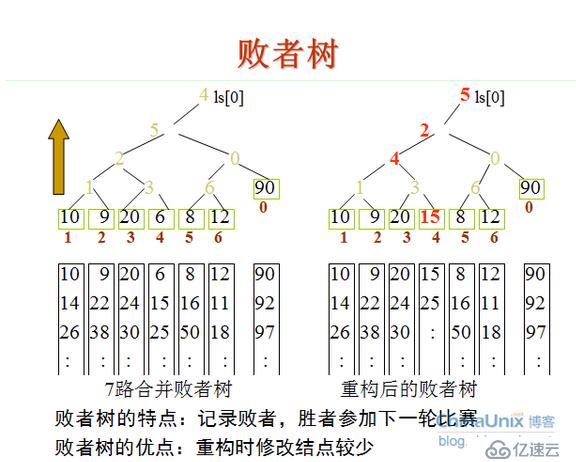
調整敗者樹

將新補充的節點與其父節點進行比較，敗者留在該父節點上，勝者繼續向上直至根節點

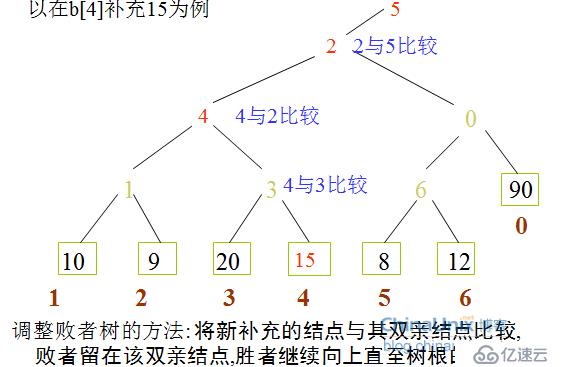
http://blog.sina.com.cn/s/blog_13a5c10be0102v1fb.html

#include <iostream>
using namespace std;

const int MINKEY = 0;

//完全二叉樹的葉子節點個數比度為2的節點個數多1
void Adjust(int* &b,int* &ls,int i,int k)
{
	//控制ls[]的下標
	int t = (i + k) / 2;//第一個非葉子結點的下標、第二個。。。
	//控制b[]的下標
	int s = i;
	for (; t > 0; t /= 2){
		if (b[ls[t]]<b[s]){
			swap(s, ls[t]);
		}
		else{
			s = s;
		}
	}
	ls[0] = s;
}
void createLoserTree(int* arr[],int k)
{
	//記錄每個數組的首元素
	int* b = new int[k+1];
	//記錄敗者的下標
	int* ls = new int[k];
	//init b[]
	for (int i = 0; i < k; ++i)
		b[i] = arr[i][0];
	b[k] = MINKEY;
	//init ls[]
	for (int i = 0; i < k; ++i)
		ls[i] = k;//最小值（絕對的勝者）的序號
	//有k個葉子節點
	//從最后一個葉子節點開始，沿著從葉子節點到根節點的路徑調整
	for (int i = k - 1; i >= 0; --i){
		Adjust(b, ls, i, k);
		for (int i = 0; i < k; ++i)
			cout << ls[i] << " ";
		cout << endl;
	}
}


int main()
{
	/*int arr1[] = { 10, 14, 26, 50 };
	int arr2[] = { 9, 22, 38 };
	int arr3[] = { 20, 24, 30 };
	int arr4[] = { 6, 15, 25 };
	int arr5[] = { 12, 11, 18 };
	int arr6[] = { 90, 92, 97 };
	int* arr[6] = { arr1, arr2, arr3, arr4, arr5, arr6 };
	createLoserTree(arr, 6);*/
	int arr1[] = { 6, 15, 25 };
	int arr2[] = { 12, 37, 48 };
	int arr3[] = { 10, 15, 16 };
	int arr4[] = { 9, 18, 20 };
	int arr5[] = { 10, 11, 40 };
	int* arr[] = { arr3, arr4, arr5, arr1, arr2 };
	createLoserTree(arr, 5);

	system("pause");
}

/*//自己分析的過程。。。（較混亂，可不看）
//createLoserTree()
for (int i = k - 1; k >= 0; --k){
	Adjust(i);
}
//Adjust(i)
int t = (i + k) / 2;//第一個非葉子結點的下標

int s = i;
for (; t >= 0; t /= 2){
	if (b[ls[t]]<b[s]){
		s = ls[t];
		ls[t] = s;
	}
	else{
		s = s;
	}
}
//i=k-1
if (b[ls[4]]<b[4]){
	s = ls[4] = 5;//勝者
	ls[4] = 4;
}勝者編號是5
else
if (b[ls[2]]<b[5])不成立
else
s = 5

//i=k-2
if (b[ls[4]]<b[3])//不成立
else{
	s = 3
}
if (b[ls[2]]<b[3]){
	s = ls[2] = 5
		ls[2] = 3
}
if (b[ls[1]]<b[5])//不成立
else
s = 5*/

2、K路歸并排序

void kMerge(int* arr[], int* arrayElementsCount, int& k, int* &ls, int* &b, int& mostMinCount)
{
    int* index = new int[k];
    for (int i = 0; i < k; ++i)
        index[i] = 0;
    for (int i = 0; i < mostMinCount; ++i){
        int s = ls[0];
        cout << b[s] << " ";
        ++index[s];
        if (index[s] < arrayElementsCount[s])
            arr[s][0] = arr[s][index[s]];
        else
            arr[s][0] = MAXKEY;
        b[s] = arr[s][0];
        Adjust(k, ls, b, s);
    }
    delete[] index;
}

3、完整代碼

#include <iostream>
using namespace std;

const int MINKEY = 0;//假設給定數組中所有數都大于0
const int MAXKEY = 200;//假設給定數組中所有數都小于200

//完全二叉樹的葉子節點個數比度為2的節點個數多1
void Adjust(int &k, int* &ls, int* &b, int i)
{
    //控制ls[]的下標
    int t = (i + k) / 2;//第一個非葉子結點的下標、第二個。。。
    //控制b[]的下標
    int s = i;
    for (; t > 0; t /= 2){
        if (b[ls[t]]<b[s]){
            swap(s, ls[t]);
        }
        else{
            s = s;
        }
    }
    ls[0] = s;
}
void createLoserTree(int* arr[],int &k, int* &ls, int* &b)
{
    //init b[]
    for (int i = 0; i < k; ++i)
        b[i] = arr[i][0];
    b[k] = MINKEY;
    //init ls[]
    for (int i = 0; i < k; ++i)
        ls[i] = k;//最小值（絕對的勝者）的序號
    //有k個葉子節點
    //從最后一個葉子節點開始，沿著從葉子節點到根節點的路徑調整
    for (int i = k - 1; i >= 0; --i){
        Adjust(k, ls, b, i);
        for (int i = 0; i < k; ++i)
            cout << ls[i] << " ";
        cout << endl;
    }
}

void kMerge(int* arr[], int* arrayElementsCount, int& k, int* &ls, int* &b, int& mostMinCount)
{
    int* index = new int[k];
    for (int i = 0; i < k; ++i)
        index[i] = 0;
    for (int i = 0; i < mostMinCount; ++i){
        int s = ls[0];
        cout << b[s] << " ";
        ++index[s];
        if (index[s] < arrayElementsCount[s])
            arr[s][0] = arr[s][index[s]];
        else
            arr[s][0] = MAXKEY;
        b[s] = arr[s][0];
        Adjust(k, ls, b, s);
    }
    delete[] index;
}

int main()
{
    int arr0[] = { 6, 15, 25 };
    int arr1[] = { 12, 37, 48, 50 };
    int arr2[] = { 10, 15, 16 };
    int arr3[] = { 9, 18, 20 };
    int arr4[] = { 10, 11, 40 };
    //6,9,10,10,11,12,15,15,16,18,20,25,37,40,48,50
    int* arr[] = { arr2, arr3, arr4, arr0, arr1 };
    int* arrayElementsCount = new int[5];
    arrayElementsCount[0] = sizeof(arr2) / sizeof(arr2[0]);
    arrayElementsCount[1] = sizeof(arr3) / sizeof(arr3[0]);
    arrayElementsCount[2] = sizeof(arr4) / sizeof(arr4[0]);
    arrayElementsCount[3] = sizeof(arr0) / sizeof(arr0[0]);
    arrayElementsCount[4] = sizeof(arr1) / sizeof(arr1[0]);
    int k = sizeof(arr) / sizeof(arr[0]);
    //記錄每個數組的首元素
    int* b = new int[k + 1];
    //記錄敗者的下標
    int* ls = new int[k];
    createLoserTree(arr, k,ls,b);
    int mostMinCount = 13;
    kMerge(arr, arrayElementsCount, k, ls, b, mostMinCount);
    delete[] b;
    delete[] ls;
    delete[] arrayElementsCount;

    system("pause");
}

后記：

堆結構：待處理的數據在樹節點中（非葉子和葉子）

敗者樹結構：待處理的數據都只在葉子節點

堆結構適用于插入式無規則的，選出最值

敗者樹結構適用于多路序列插入，選出最值