您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章將為大家詳細講解有關JavaScript 中怎么實現一個二叉樹算法,文章內容質量較高,因此小編分享給大家做個參考,希望大家閱讀完這篇文章后對相關知識有一定的了解。
二叉樹和二叉搜索樹介紹
二叉樹中的節點最多只能有2個子節點,一個是左側子節點,一個是右側子節點,這樣定義的好處是有利于我們寫出更高效的插入,查找,刪除節點的算法。二叉搜索樹是二叉樹的一種,但是它只允許你在左側子節點存儲比父節點小的值,但在右側節點存儲比父節點大的值。接下來我們將按照這個思路去實現一個二叉搜索樹。
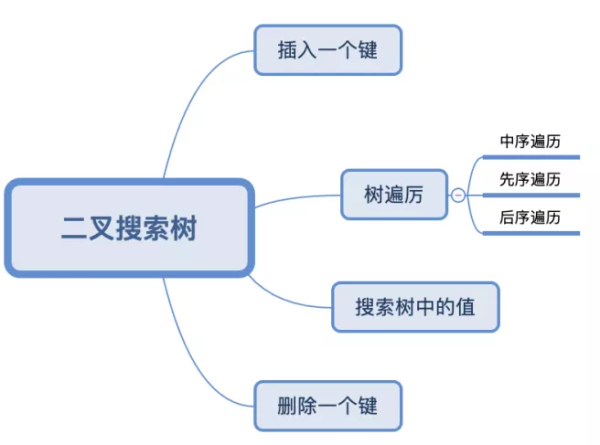
1. 創建BinarySearchTree類
這里我們將使用構造函數去創建一個類:
function BinarySearchTree(){ // 用于創建節點的類 let Node = function(key) { this.key = key; this.left = null; this.right = null; } // 根節點 let root = null; }我們將使用和鏈表類似的指針方式去表示節點之間的關系,如果不了解鏈表,請看我后序的文章《如何實現單向鏈表和雙向鏈表》。
2.插入一個鍵
// 插入一個鍵 this.insert = function(key) { let newNode = new Node(key); root === null ? (root = newNode) : (insertNode(root, newNode)) }向樹中插入一個新的節點主要有以下三部分:1.創建新節點的Node類實例 --> 2.判斷插入操作是否為根節點,是根節點就將其指向根節點 --> 3.將節點加入非根節點的其他位置。
insertNode的具體實現如下:
function insertNode(node, newNode){ if(newNode.key < node.key) { node.left === null ? (node.left = newNode) : (insertNode(node.left, newNode)) }else { node.right === null ? (node.right = newNode) : (insertNode(node.right, newNode)) } }這里我們用到遞歸,接下來要實現的search,del等都會大量使用遞歸,所以說不了解的可以先自行學習了解。我們創建一個二叉樹實例,來插入一個鍵:
let tree = new BinarySearchTree(); tree.insert(20); tree.insert(21); tree.insert(520); tree.insert(521);
插入的結構會按照二叉搜索樹的規則去插入,結構類似于上文的第一個樹圖。
樹的遍歷
訪問樹的所有節點有三種遍歷方式:中序,先序和后序。
中序遍歷:以從最小到最大的順序訪問所有節點
先序遍歷:以優先于后代節點的順序訪問每個節點
后序遍歷:先訪問節點的后代節點再訪問節點本身
根據以上的介紹,我們可以有以下的實現代碼。
1 中序排序
this.inOrderTraverse = function(cb){ inOrderTraverseNode(root, cb); } // 輔助函數 function inOrderTraverseNode(node, cb){ if(node !== null){ inOrderTraverseNode(node.left, cb); cb(node.key); inOrderTraverseNode(node.right, cb); } }使用中序遍歷可以實現對樹進行從小到大排序的功能。
2 先序排序
// 先序排序 --- 優先于后代節點的順序訪問每個節點 this.preOrderTraverse = function(cb) { preOrderTraverseNode(root, cb); } // 先序排序輔助方法 function preOrderTraverseNode(node, cb) { if(node !== null) { cb(node.key); preOrderTraverseNode(node.left, cb); preOrderTraverseNode(node.right, cb); } }使用先序排序可以實現結構化輸出的功能。
3 后序排序
// 后續遍歷 --- 先訪問后代節點,再訪問節點本身 this.postOrderTraverse = function(cb) { postOrderTraverseNode(root, cb); } // 后續遍歷輔助方法 function postOrderTraverseNode(node, cb) { if(node !== null){ postOrderTraverseNode(node.left, cb); postOrderTraverseNode(node.right, cb); cb(node.key); } }后序遍歷可以用于計算有層級關系的所有元素的大小。
搜索樹中的值
在樹中有三種經常執行的搜索類型:最大值,最小值,特定的值。
1 最小值
最小值通過定義可以知道即是左側樹的最底端的節點,具體實現代碼如下:
// 最小值 this.min = function(){ return minNode(root) } function minNode(node) { if(node) { while(node && node.left !== null){ node = node.left; } return node.key } return null }相似的,實現最大值的方法如下:
// 最大值 this.max = function() { return maxNode(root) } function maxNode(node) { if(node){ while(node && node.right !== null){ node = node.right; } return node.key } return null }2.搜索一個特定的值
// 搜索樹中某個值 this.search = function(key) { return searchNode(root, key) } // 搜索輔助方法 function searchNode(node, key){ if(node === null) { return false } if(key < node.key) { return searchNode(node.left, key) } else if(key > node.key) { return searchNode(node.right, key) }else { return true } }3 移除一個節點
this.remove = function(key){ root = removeNode(root, key); } // 發現最小節點 function findMinNode(node) { if(node) { while(node && node.left !== null){ node = node.left; } return node } return null } // 移除節點輔助方法 function removeNode(node, key) { if(node === null) { return null } if(key < node.key){ node.left = removeNode(node.left, key); return node } else if( key > node.key){ node.right = removeNode(node.right, key); return node } else { // 一個頁節點 if(node.left === null && node.right === null) { node = null; return node } // 只有一個子節點的節點 if(node.left === null) { node = node.right; return node }else if(node.right === null) { node = node.left; return node } // 有兩個子節點的節點 let aux = findMinNode(node.right); node.key = aux.key; node.right = removeNode(node.right, aux.key); return node } }刪除節點需要考慮的情況比較多,這里我們會使用和min類似的實現去寫一個發現最小節點的函數,當要刪除的節點有兩個子節點時,我們要將當前要刪除的節點替換為子節點中最大的一個節點的值,然后將這個子節點刪除。
關于JavaScript 中怎么實現一個二叉樹算法就分享到這里了,希望以上內容可以對大家有一定的幫助,可以學到更多知識。如果覺得文章不錯,可以把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。