您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“順序查找和二叉查找的詳細介紹”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“順序查找和二叉查找的詳細介紹”吧!
本文主要先介紹查找的概念,然后介紹最簡單的查找算法——順序查找,最后介紹二分查找。
我們平常做很多事情,都會涉及到大量的增刪改查操作。比如一個用戶管理系統,會涉及用戶注冊(增)、用戶注銷(刪)、修改用戶信息(改)、查找用戶(查),其中“刪”和“改”要依賴“查”操作。
下面重點來介紹一下查找這個重要的操作。
現給你一個點名冊,讓你查找一個學生。我們的做法是:根據這個學生的姓名或者學號,在點名冊中一個個的比對,直到找到一個學號或姓名符合條件的學生為止,否則就可以說點名冊中沒有該學生。
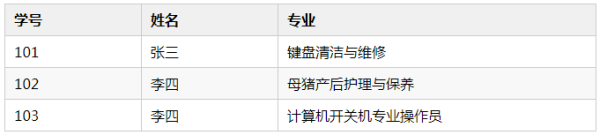
點名冊是一個集合,也可稱之為查找表,其中有大量同一類型的元素,也可稱之為記錄——學生。學生中可能有重名的,但不會有重學號的,也即,一個學號唯一對應一個學生,一個姓名可能對應多個學生。如果我們根據學號找,只要點名冊中有,那么就可以找到唯一一個符合條件的學生。如果我們根據姓名找,那么我們就可能找到多個符合條件的學生。
像學號和姓名這種可以標識一個學生的值,我們稱之為關鍵字,學號這種唯一標識一個元素的值為主關鍵字,姓名這種可能標識若干元素的值為次關鍵字。當集合中的元素只有一個數據項時,其關鍵字即為該數據元素的值。
比如數組[1, 2, 3, 4, 5, 6, 7, 8, 9],其元素只有一個數據項,關鍵字即元素值本身;而點名冊中的元素——學生,卻有三個數據項——學號、姓名、專業,其中學號、姓名為關鍵字。
如果你學過數據庫,那么以上概念很容易理解。
所謂查找,通俗點說就是在一大群元素(集合 / 查找表)中,依照某個查找依據,找一個特定的、符合要求的元素(記錄)。
如果找到了,即查找成功,返回元素的信息;
如果找遍所有元素還沒找到,說明這群元素中沒有符合要求的元素,即查找失敗,返回一個可以明顯標記失敗的值,比如“空記錄”或“空指針”。
所謂查找依據,就是給定一個目標值,比較該目標值和關鍵字是否相等。這就要求目標值和關鍵字的類型要相同。
順序查找是我們最容易想到的查找方式,上面的點名冊例子中,查找一個學生就是用的就是順序查找。
從集合中的第一個元素開始至最后一個元素,逐個比較其關鍵字和目標值。
若某個關鍵字和目標值相等,則查找成功,返回所查元素的信息;
若沒有一個關鍵字和目標值相等,則查找失敗,返回失敗標識值。
比如,給定一個數組[11, 8, 4, 6, 9, 1, 16, 22, 14, 10],給定目標值 key,若找到,則返回其數組下標;否則,返回 -1:

只需從下標 0 開始遍歷整個數組進行比較即可:
/** * @description: 從頭到尾遍歷整個數組,查找目標值 key,返回其下標 index * @param {int} *array 數組 為了說明問題簡單,這里的數組元素不重復 * @param {int} length 數組長度 * @param {int} key 目標值 * @return {int} 如果找到,返回目標值下標;否則返回 -1 */ int sequential_search(int *array, int length, int key) { for (int index = 0; index < length; index++) { if (array[index] == key) { return index; } } return -1; }以上代碼存在可優化的地方,因為每次比較之前要判斷數組是否越界:index < length,增加哨兵則可以避免這一步比較。
所謂哨兵,是一種形象的說法,將其放在數組頭或尾,用來標記結束,當遍歷到“哨兵”時,就說明數組中沒有目標值,查找失敗。
為此,我們要特意在數組中留出一個位置給“哨兵”,并且把哨兵的值設置為目標值:
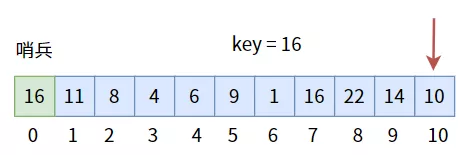
像這樣,從另一側往“哨兵”一側遍歷。如果數組中有目標值,則一定能找到;如果數組中沒有目標值,那么就會遍歷至“哨兵”而停下,因為“哨兵”的值就是目標值,所以返回下標為 0 時,意味著查找失敗。
/** * @description: 順序查找改進,增加哨兵 * @param {int} *array array[0] 不存放數據元素,充當哨兵 * @param {int} length 數組長度 * @param {int} key 目標值 * @return {int} 返回0,即哨兵下標,則查找失敗;否則成功 */ int sequential_search_pro(int *array, int length, int key) { array[0] = key; // 哨兵 int index = length - 1; while (array[index] != key) { index--; } return index; }在一側放置“哨兵”的做法避免了每次遍歷進行的數組越界檢查,這樣能提高效率。你可能會問就一句比較能提高多少效率?蚊子腿再小也是肉,而且當數據量很多時,這些“蚊子腿”就會積累成“大象腿”了。
以上就是順序查找的基本內容,雖然加了“哨兵”可以小小地優化一下,但當數據量極大時,仍然改變不了這種查找方法效率低下的事實。
因為我們是從一頭到另一頭“順序遍歷”,所以有時候可能目標值就在第一個位置,只查找一次就找到了,仿佛是天選之子;但有時候可能目標值在最后一個位置,那就需要把所有元素都查找一遍才行,當有千萬、億條數據時,這種就太可怕了。
當然,優點也有:算法簡單好理解、適合數據量小的情況使用(使用時盡量把常用數據排在前面,這樣可以提高效率)。
回到上面舉得那個點名冊的例子,那樣一個個地找學號或姓名實在是太慢了,有沒有什么更快的方法呢?
其實,在日常生活中的點名冊更多的是已排序的,比如按姓氏首字母、按學號大小排序,這樣一來,在找名字或找學號的時候就能有一個大致的區域了,而不必從頭到尾一個個地找。
所以,排好序的集合是便于查找的。下面介紹一種利用已排序的查找——二分查找(或折半查找)。
所謂二分查找,關鍵在“二分”“折半”上,顧名思義,不斷將集合進行二分(折半)拆分,以此將集合拆分幾個區域,然后在某個區域中查找。前提條件是集合中的元素是有序的,元素必須采用順序表(數組)存儲。
二分查找思想:
在有序順序表中,取中間元素,將有序順序表分為左半區和右半區,比較中間元素的關鍵字和目標值 key 是否相等:
1.如果相等,則查找成功,返回中間元素的信息;
2.如果不相等,說明目標值 key 在左半區或右半區:
若目標值 key小于中間元素的關鍵字,則來到左半區;
若目標值 key 大于中間元素的關鍵字,則來到右半區;
不斷在各半區中重復上述過程,直到查找成功;否則,則集合中無目標值,查找失敗。
下面結合實例,看一下具體過程。
這是一個有序的數組,我們要查找 33:

要想將數組分為左右半區,需要三個標致:最左標志位 left、最右標志位 right和中間標志位 mid。其中 mid = (left + right) / 2,確定了 mid 的值之后,與目標值 key進行比較:
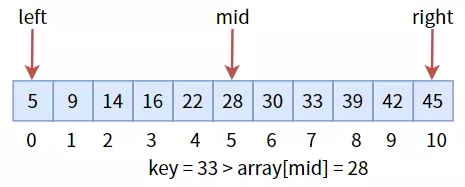
中間值 28 小于目標值key,說明目標值在右半區,所以更新三個標志位,進入右半區,然后繼續比較:
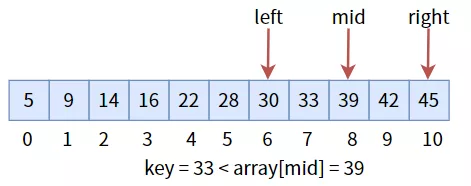
中間值 39 大于目標值key,更新三個標志位,進入左半區:
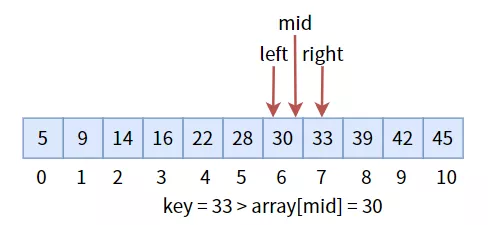
中間值 30 小于目標值key,更新三個標志位,進入右半區:

中間值 33 等于目標值key,返回其下標,即 mid。
具體代碼如下:
/** * @description: 二分查找 * @param {int} *array 有序數組 * @param {int} length 數組長度 * @param {int} key 目標值,和關鍵字比較 * @return {int} 返回目標值下標;若查找失敗,則返回 -1 */ int binary_search(int *array, int length, int key) { int left, mid, right; left = 0; right = length - 1; while (left <= right) { mid = (left + right) / 2; // 中間下標 if (key < array[mid]) { // key 比中間值小 right = mid - 1; // 更新最右下標,進入左半區 } else if (key > array[mid]) { // key 比中間值大 left = mid + 1; // 更新最左下標,進入右半區 } else { return mid; // key 等于中間值,返回其下標 } } return -1; //未找到,返回 -1 }二分查找的精髓在于中間標志位 mid 把有序順序表一分為二,通過比較中間值和目標值的大小關系,能夠篩選掉一半的數據,相當于減少了一半的工作量。
上例只比較了四次,就找到了目標值,如果使用順序查找,則需要八次。
可以看出,二分查找的效率相較于順序查找有了很大提高,但美中不足的是二分查找必須要求元素有序。在元素的有序狀態不變化或不經常變化的情景下,二分查找非常合適;但是如果涉及到頻繁的插入和刪除操作,就意味著元素的有序狀態會被頻繁破壞,這樣一來,我們就不得不花精力去維護元素的有序狀態,自然又會降低效率,所以要根據實際情況靈活取舍。
以上就是順序查找和二分查找的內容。
到此,相信大家對“順序查找和二叉查找的詳細介紹”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。