您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹python如何解決微分方程,文中介紹的非常詳細,具有一定的參考價值,感興趣的小伙伴們一定要看完!
對于一些微分方程來說,數值解法對于求解具有很好的幫助,因為難以求得其原方程。
比如方程:
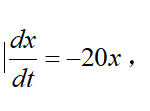
但是我們知道了它的初始條件,這對于我們疊代求解很有幫助,也是必須的。
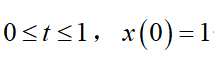
那么現在我們也用Python去解決這一些問題,一般的數值解法有歐拉法、隱式梯形法等,我們也來看看這些算法對疊代的精度有什么區別?
```python
```python
import numpy as np
from scipy.integrate import odeint
from matplotlib import pyplot as plt
import os
#先從odeint函數直接求解微分方程
#創建歐拉法的類
class Euler:
#構造方法,當創建對象的時候,自動執行的函數
def __init__(self,h,y0):
#將對象與對象的屬性綁在一起
self.h = h
self.y0 = y0
self.y = y0
self.n = 1/self.h
self.x = 0
self.list = [1]
#歐拉法用list列表,其x用y疊加儲存
self.list2 = [1]
self.y1 = y0
#改進歐拉法用list2列表,其x用y1疊加儲存
self.list3 = [1]
self.y2 = y0
#隱式梯形法用list3列表,其x用y2疊加儲存
#歐拉法的算法,算法返回t,x
def countall(self):
for i in range(int(self.n)):
y_dere = -20*self.list[i]
#歐拉法疊加量y_dere = -20 * x
y_dere2 = -20*self.list2[i] + 0.5*400*self.h*self.list2[i]
#改進歐拉法疊加量 y_dere2 = -20*x(k) + 0.5*400*delta_t*x(k)
y_dere3 = (1-10*self.h)*self.list3[i]/(1+10*self.h)
#隱式梯形法計算 y_dere3 = (1-10*delta_t)*x(k)/(1+10*delta_t)
self.y += self.h*y_dere
self.y1 += self.h*y_dere2
self.y2 =y_dere3
self.list.append(float("%.10f" %self.y))
self.list2.append(float("%.10f"%self.y1))
self.list3.append(float("%.10f"%self.y2))
return np.linspace(0,1,int(self.n+1)), self.list,self.list2,self.list3
step = input("請輸入你需要求解的步長:")
step = float(step)
work1 = Euler(step,1)
ax1,ay1,ay2,ay3 = work1.countall()
#畫圖工具plt
plt.figure(1)
plt.subplot(1,3,1)
plt.plot(ax1,ay1,'s-.',MarkerFaceColor = 'g')
plt.xlabel('橫坐標t',fontproperties = 'simHei',fontsize =20)
plt.ylabel('縱坐標x',fontproperties = 'simHei',fontsize =20)
plt.title('歐拉法求解微分線性方程步長為'+str(step),fontproperties = 'simHei',fontsize =20)
plt.subplot(1,3,2)
plt.plot(ax1,ay2,'s-.',MarkerFaceColor = 'r')
plt.xlabel('橫坐標t',fontproperties = 'simHei',fontsize =20)
plt.ylabel('縱坐標x',fontproperties = 'simHei',fontsize =20)
plt.title('改進歐拉法求解微分線性方程步長為'+str(step),fontproperties = 'simHei',fontsize =20)
plt.subplot(1,3,3)
plt.plot(ax1,ay3,'s-.',MarkerFaceColor = 'b')
plt.xlabel('橫坐標t',fontproperties = 'simHei',fontsize =20)
plt.ylabel('縱坐標x',fontproperties = 'simHei',fontsize =20)
plt.title('隱式梯形法求解微分線性方程步長為'+str(step),fontproperties = 'simHei',fontsize =20)
plt.figure(2)
plt.plot(ax1,ay1,ax1,ay2,ax1,ay3,'s-.',MarkerSize = 3)
plt.xlabel('橫坐標t',fontproperties = 'simHei',fontsize =20)
plt.ylabel('縱坐標x',fontproperties = 'simHei',fontsize =20)
plt.title('三合一圖像步長為'+str(step),fontproperties = 'simHei',fontsize =20)
ax = plt.gca()
ax.legend(('$Eular$','$fixed Eular$','$trapezoid$'),loc = 'lower right',title = 'legend')
plt.show()
os.system("pause")對于歐拉法,它的疊代方法是:
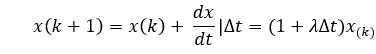
改進歐拉法的疊代方法:
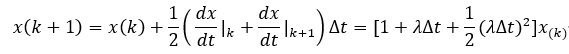
隱式梯形法:
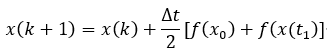
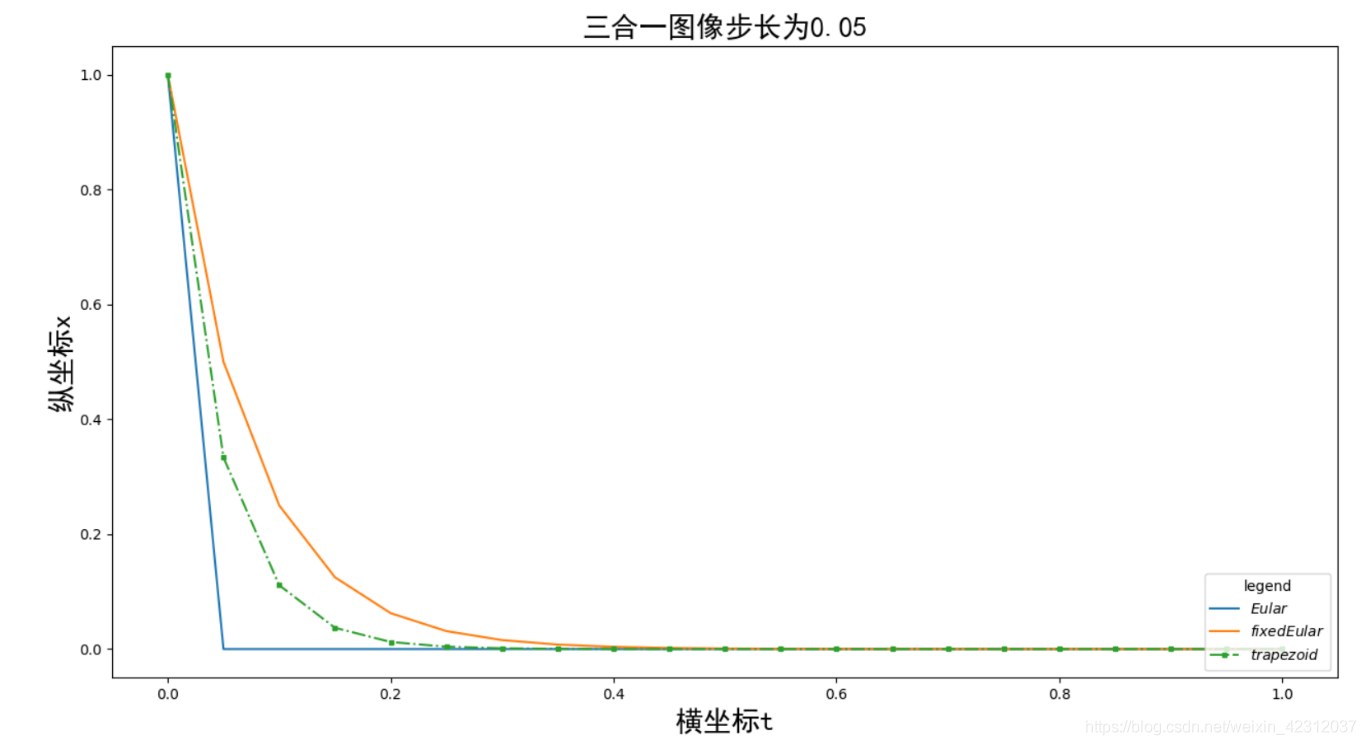
對于不同的步長,其求解的精度也會有很大的不同,我先放一幾張結果圖:
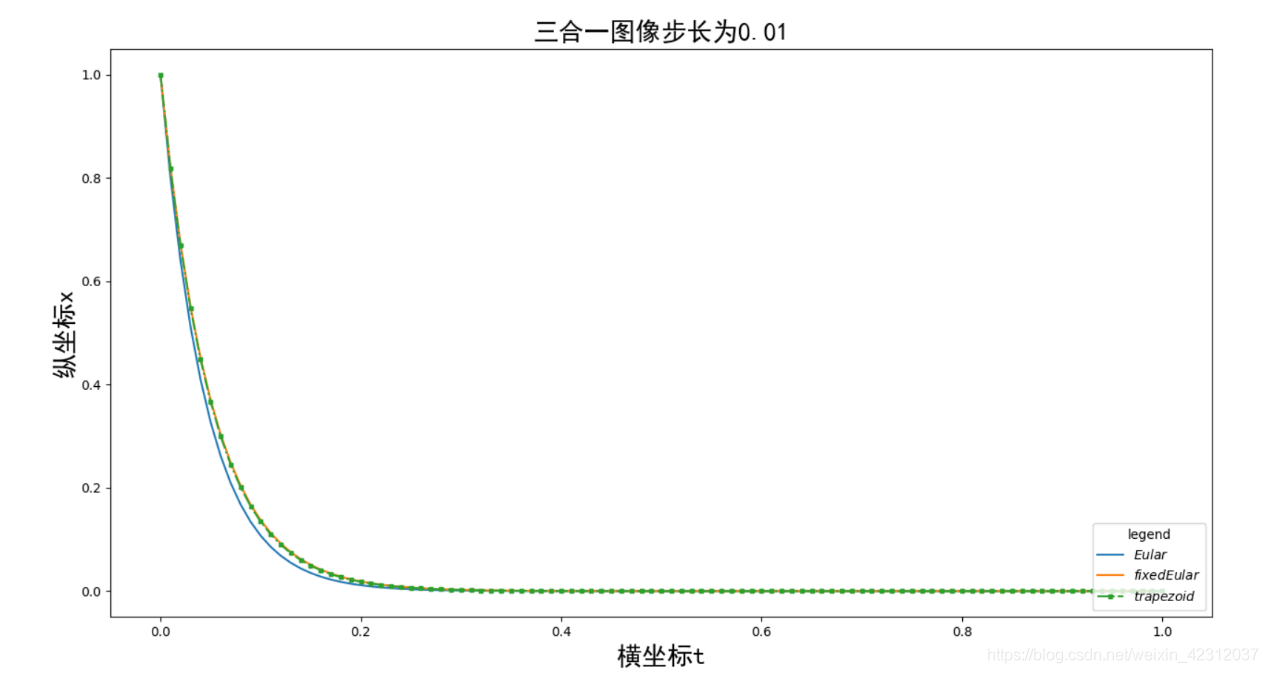
補充:基于python的微分方程數值解法求解電路模型
安裝numpy(用于調節range) 和 matplotlib(用于繪圖)
在命令行輸入
pip install numpy pip install matplotlib
無損害,電容電壓為5V,電容為0.01F,電感為0.01H的并聯諧振電路
電路模型1
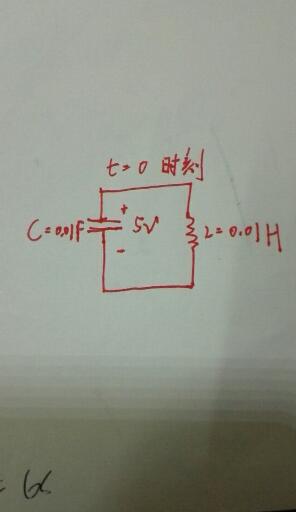
微分方程1
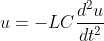
帶電阻損耗的電容電壓為5V,電容為0.01F,電感為0.01H的的并聯諧振
電路模型2
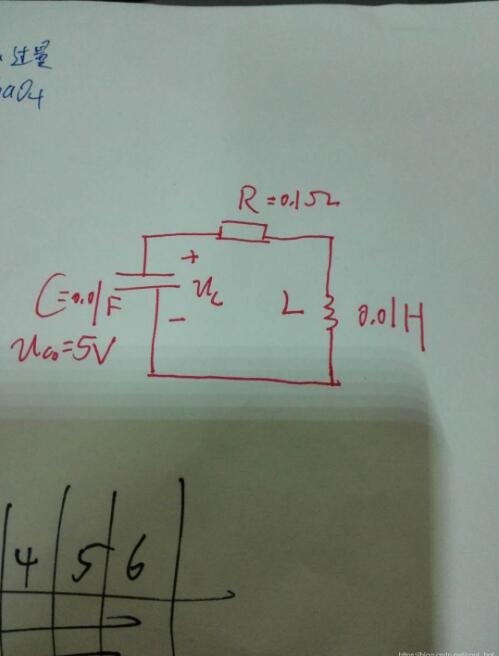
微分方程2
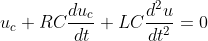
import numpy as np
import matplotlib.pyplot as plt
L = 0.01 #電容的值 F
C = 0.01 #電感的值 L
u_0 = 5 #電容的初始電壓
u_dot_0 = 0
def equition(u,u_dot):#二階方程
u_double_dot = -u/(L*C)
return u_double_dot
def draw_plot(time_step,time_scale):#時間步長和范圍
u = u_0
u_dot = u_dot_0 #初始電壓和電壓的一階導數
time_list = [0] #時間lis
Votage = [u] #電壓list
plt.figure()
for time in np.arange(0,time_scale,time_step):#使用歐拉數值計算法 一階近似
u_double_dot = equition(u,u_dot) #二階導數
u_dot = u_dot + u_double_dot*time_step #一階導數
u = u + u_dot*time_step #電壓
time_list.append(time) #結果添加
Votage.append(u) #結果添加
print(u)
plt.plot(time_list,Votage,"b--",linewidth=1) #畫圖
plt.show()
plt.savefig("easyplot.png")
if __name__ == '__main__':
draw_plot(0.0001,1)import numpy as np
import matplotlib.pyplot as plt
L = 0.01 #電容的值 F
C = 0.01 #電感的值 L
R = 0.1 #電阻值
u_0 = 5 #電容的初始電壓
u_dot_0 = 0
def equition(u,u_dot):#二階方程
u_double_dot =(-R*C*u_dot -u)/(L*C)
return u_double_dot
def draw_plot(time_step,time_scale):#時間步長和范圍
u = u_0
u_dot = u_dot_0 #初始電壓和電壓的一階導數
time_list = [0] #時間lis
Votage = [u] #電壓list
plt.figure()
for time in np.arange(0,time_scale,time_step):#使用歐拉數值計算法 一階近似
u_double_dot = equition(u,u_dot) #二階導數
u_dot = u_dot + u_double_dot*time_step #一階導數
u = u + u_dot*time_step #電壓
time_list.append(time) #結果添加
Votage.append(u) #結果添加
print(u)
plt.plot(time_list,Votage,"b-",linewidth=1) #畫圖
plt.show()
plt.savefig("result.png")
if __name__ == '__main__':
draw_plot(0.0001,1)模型1
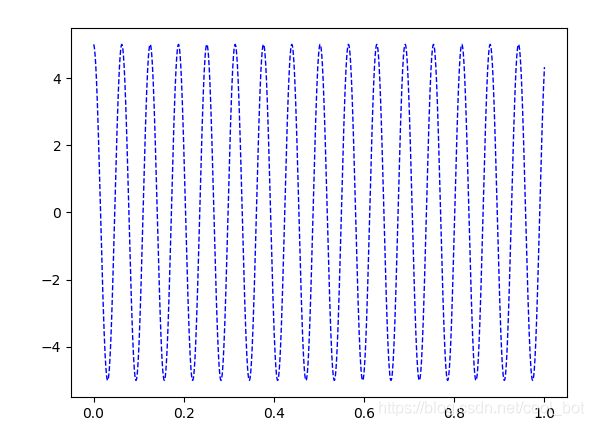
縱軸為電容兩端電壓,橫軸為時間與公式計算一致
模型2結果
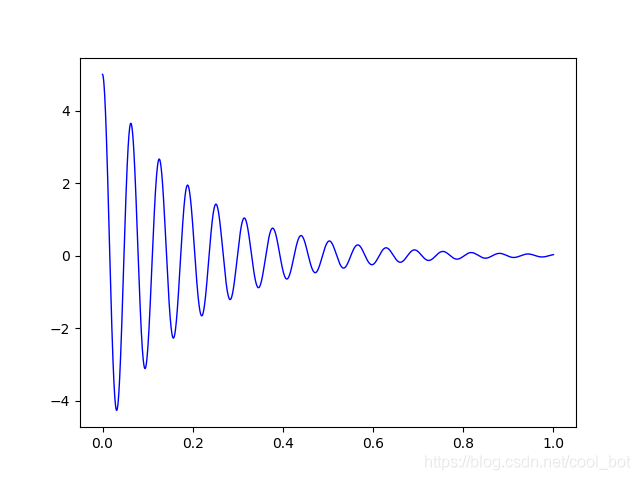
為電容兩端電壓,橫軸為時間標題
最后我們可以根據調節電阻到達不同的狀態
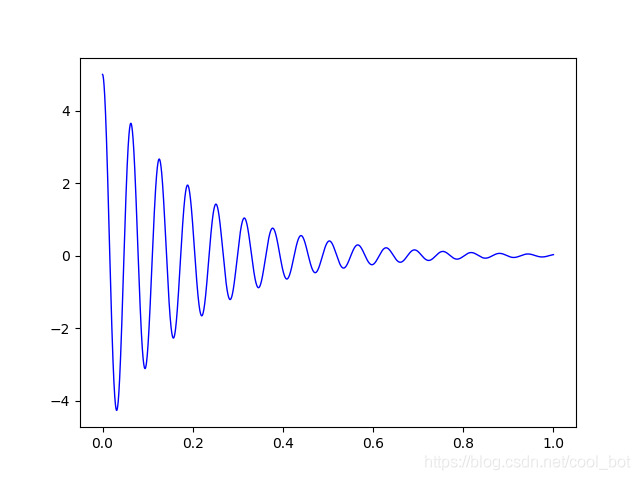
R=0.01,欠阻尼
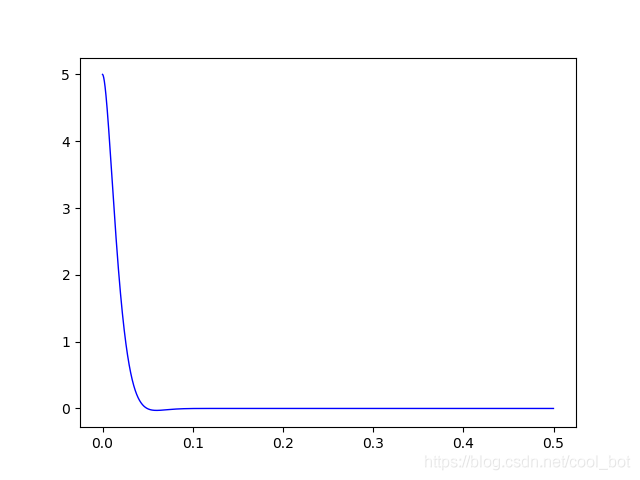
R=1.7,臨界阻尼
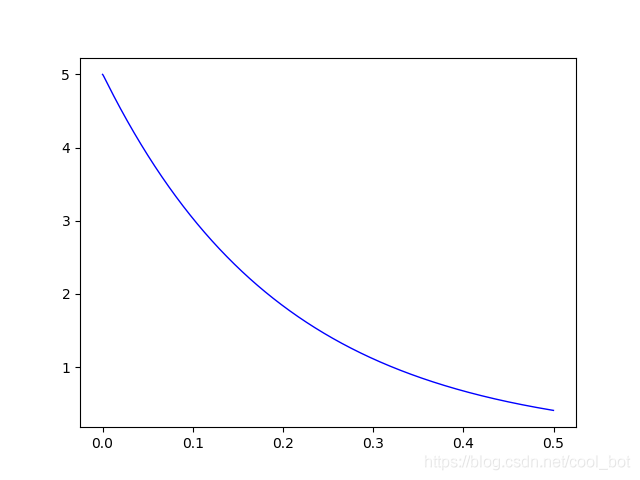
R=100,過阻尼
1、云計算,典型應用OpenStack。2、WEB前端開發,眾多大型網站均為Python開發。3.人工智能應用,基于大數據分析和深度學習而發展出來的人工智能本質上已經無法離開python。4、系統運維工程項目,自動化運維的標配就是python+Django/flask。5、金融理財分析,量化交易,金融分析。6、大數據分析。
以上是“python如何解決微分方程”這篇文章的所有內容,感謝各位的閱讀!希望分享的內容對大家有幫助,更多相關知識,歡迎關注億速云行業資訊頻道!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。