溫馨提示×
您好，登錄后才能下訂單哦！
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好，登錄后才能下訂單哦！
這篇文章主要介紹了css3中矩陣如何使用，具有一定借鑒價值，感興趣的朋友可以參考下，希望大家閱讀完這篇文章之后大有收獲，下面讓小編帶著大家一起了解一下。
css3 矩陣變化. 應用格式為:
transform: matrix(a,b,c,d,e,f);
對應于就是:
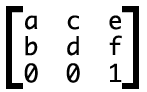
實際應用中的轉換就是:
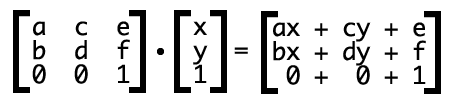
其中:
ax+cy+e = 橫坐標
bx+dy+f = 縱坐標
為什么會多出 0 0 1呢？ 因為, 為了湊參數.
translate 矩陣
基本格式為:
transform: matrix(1, 0, 0, 1, X, Y); // X 橫向平移, Y 縱向平移
scale 矩陣
scale(縮放) 的矩陣也挺簡單.
// 將 X 軸縮放 A 倍 // 將 Y 軸縮放 B 倍 matrix(A, 0, 0, B, 0,0);
當然, 如果你在最后兩位寫上數字, 代表著, 先縮放再平移.
// 得到: X 軸 = 0.3*x + 100 // 得到: Y 軸 = 0.2*x + 200 matrix(0.3,0,0,0.2,100,200);
rotate 矩陣
rotate 實際上和三角函數有很大的關系. 首先,確定你的旋轉角(順時針旋轉). 然后, 計算 sinθ 和 cosθ. 最后的矩陣公式為:
matrix(cosθ,sinθ,-sinθ,cosθ,0,0) // 就是 cs-sc
skew 矩陣
skew(拉伸) 矩陣也是三角函數, 不過, 用到的是tanθ. 格式為:
// 將 Y 軸向 X 軸傾斜 A° // 將 X 軸向 Y 軸傾斜 B° matrix(1,tan(A),tan(B),1,0,0)
3D變換矩陣
3D 變換是 4*4 的矩陣. 他和 2D 類似,只是, 多出一個Z。 // 這是縮放的3D矩陣
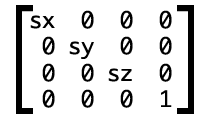
對應的 css 寫法為:
transform: matrix3d(sx, 0, 0, 0, 0, sy, 0, 0, 0, 0, sz, 0, 0, 0, 0, 1)
感謝你能夠認真閱讀完這篇文章，希望小編分享的“css3中矩陣如何使用”這篇文章對大家有幫助，同時也希望大家多多支持億速云，關注億速云行業資訊頻道，更多相關知識等著你來學習!
免責聲明：本站發布的內容（圖片、視頻和文字）以原創、轉載和分享為主，文章觀點不代表本網站立場，如果涉及侵權請聯系站長郵箱：is@yisu.com進行舉報，并提供相關證據，一經查實，將立刻刪除涉嫌侵權內容。
