JS數據結構之鏈表的優點是什么

這篇文章給大家分享的是有關JS數據結構之鏈表的優點是什么的內容。小編覺得挺實用的，因此分享給大家做個參考，一起跟隨小編過來看看吧。

在本文中，我們將討論如何將鏈表存儲在數據庫中，實現鏈表的添加和刪除，查找以及反轉鏈表等操作。 在實現鏈表之前，需要知道相比數組和對象，鏈表的優點是什么。

我們知道，數組中的元素以索引編號和順序存儲在數據庫中：

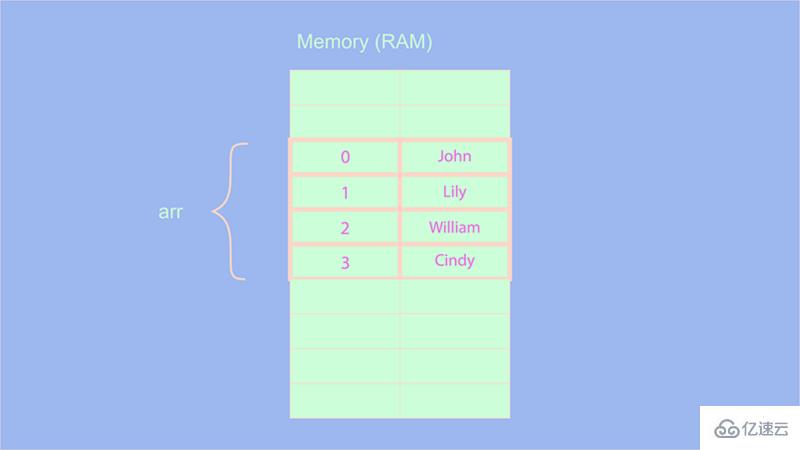
在使用數組時，在開始或特定索引處添加/刪除元素這樣的操作可能是一項性能較低的任務，因為我們必須移動所有其他元素的索引，造成這種原因是由數組的編號索引特性導致的。

使用對象可以解決上述問題。 由于在對象中，元素存儲位置是隨機的，因此，在執行諸如在開始處或特定索引處添加/刪除元素之類的操作時，無需移動元素的索引：

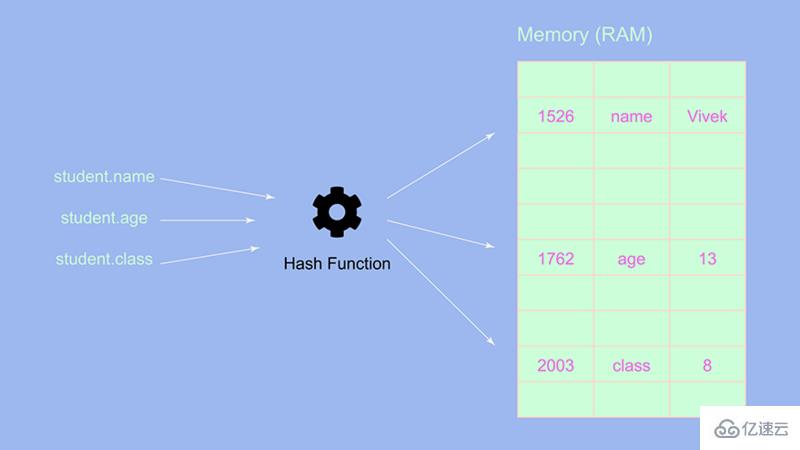
盡管在對象中添加和刪除元素速度很快，但是從上圖可以看出，在進行迭代操作時，對象并不是最佳選擇，因為對象的元素存儲在隨機位置。 因此，迭代操作可能需要很長時間。 這是鏈表引出的原因。

那么什么是鏈表呢 ?

從名字本身可以看出它是一個以某種方式鏈表。 那么它是如何鏈接的，列表包含什么呢？

鏈表由具有兩個屬性的節點組成：數據和指針。

節點內的指針指向列表中的下一個節點。 鏈表中的第一個節點稱為head。 為了更好地理解，讓我們看一下描述鏈表圖示：

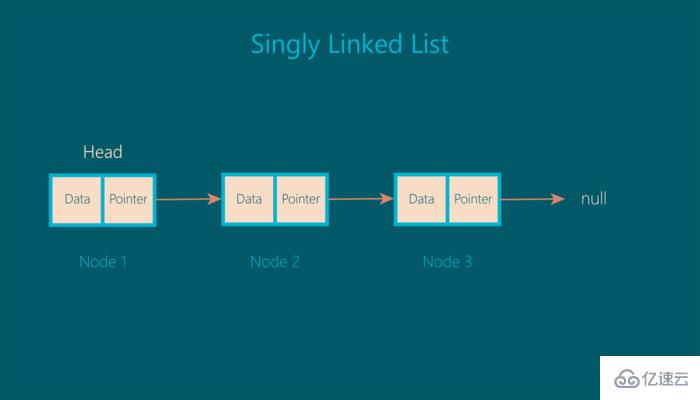
從上圖可以看出，每個節點都有兩個屬性，data和pointer。 指針指向列表中的下一個節點，最后一個節點的指針指向null，上圖是一個單鏈表 ?。

鏈表和對象時有很大的不同。 在鏈表中，每個節點都通過指針(pointer)連接到下一個節點。 因此，我們在鏈表的每個節點之間都有連接，而在對象中，鍵值對是隨機存儲的，彼此之間沒有連接。

接著，我們實現一個存儲整數的鏈表。 由于 JS 不提供內置的鏈表支持，因此我們將使用對象和類來實現鏈表 ?

class Node {
  constructor (value) {
    this.value = value
    this.next = null
  }
}

class LinkedList {
  constructor () {
    this.head = null
    this.tail = this.head
    this.length = 0
  }
  append (value) {
  }

  prepend (value) {

  }

  insert (value, index) {

  }

  lookup (index) {

  }

  remove (index) {

  }

  reverse () {
    
  }
}

在上面的代碼中，我們創建了兩個類，一個用于來鏈表本身，一個是節點本身。 如我們所討論的，每個節點將具有兩個屬性，一個值和一個指針(對應 next 字段)。

LinkedList類包含三個屬性，head(初始值為null)，用于存儲鏈表的最后一個節點的tail(也指向null)和用于保存鏈表長度的length屬性。接著，我們來實現里面的方法 ?。

append (按順序添加值)

這個函數將一個節點添加到鏈表的末尾。為了實現這個函數，我們需要理解它需要執行的一些操作：

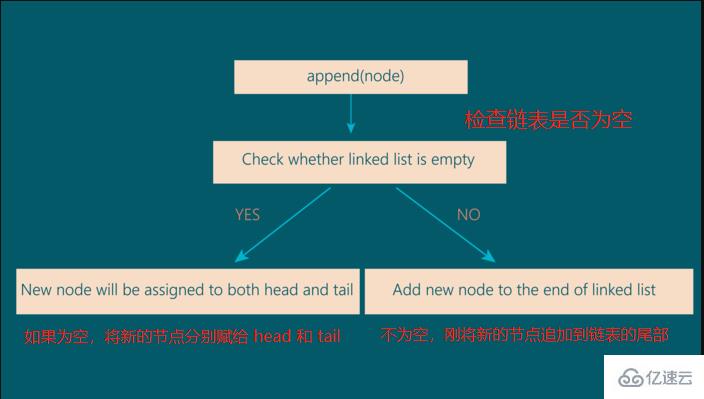
從上圖中，我們可以通過以下方式實現append函數：

  append (value) {
    const newNode = new Node(value)
    if (!this.head) {
      this.head = newNode
      this.tail = newNode
    } else {
      this.tail.next = newNode
      this.tail = newNode
    }
    this.length++
  }

簡單的對 append 方法解釋一下 ?：

const linkedList1 = new LinkedList()
linkedList1.append(2)

檢查head是否指向null，此時的head指向null，因此我們創建一個新對象，并將新對象分配給head和tail:

let node = new Node(2)
this.head = newNode
this.tail = newNode

現在，head 和 tail 都指向同一個對象，這一點很重要，要記住。

接著，我們再向鏈表添加兩個值：

linkedList1.append(3)
linkedList1.append(4)

現在，head 不指向null，所以我們進入append函數的else分支：

this.tail.next = node

由于head 和tail 都指向同一個對象，tail的變化都會導致head對象的變化，這是JS 中對象的工作方式。在JavaScript中，對象是通過引用傳遞的，因此 head 和tail都指向存儲對象的相同地址空間。上面這行代碼相當于

this.head.next = node;

下一行：

this.tail = node

現在，在執行完上面的代碼行之后，this.head.next和this.tail指向同一對象，因此，每當我們添加新節點時，head對象都會自動更新。

執行三次append之后，linkedList1 的結構應該是這樣的：

head: {value: 2 , next: {value: 3, next: {value: 4,next: null}}}
tail : {value: 4, next: null}
length:3

從上面的代碼中我們可以看到，鏈表的append函數的復雜度是O(1)，因為我們既不需要移動索引，也不需要遍歷鏈表。

我們來看下一個函數 ?

prepend (將值添加到鏈表的開頭)

為了實現此函數，我們使用Node類創建一個新節點，并將該新節點的下一個對象指向鏈表的head 。 接下來，我們將新節點分配給鏈表的head：

與append函數一樣，這個函數的復雜度也是O(1)。

  prepend (value) {
  const node = new Node(value)

  node.next = this.head
  this.head = node
  this.length++
}

就像append函數一樣，此函數的復雜度也為O(1)。

insert (在特定索引處添加值)

在實現此函數之前，我們先看看它的一個轉化過程。因此，出于理解目的，我們先創建一個值很少的鏈表，然后可視化insert函數。 insert  函數接受兩個參數，值和索引:

let linkedList2 = new LinkedList()
linkedList2.append(23)
linkedList2.append(89)
linkedList2.append(12)
linkedList2.append(3)

linkedList2.insert(45,2)

第1步：

遍歷鏈表，直到到達index-1位置:

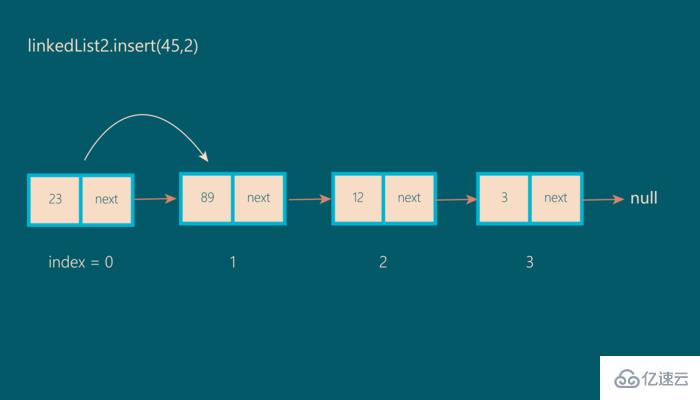
第2步：

將索引為1的節點的指針（在本例中為89）分配給新節點（在本例中為45）：

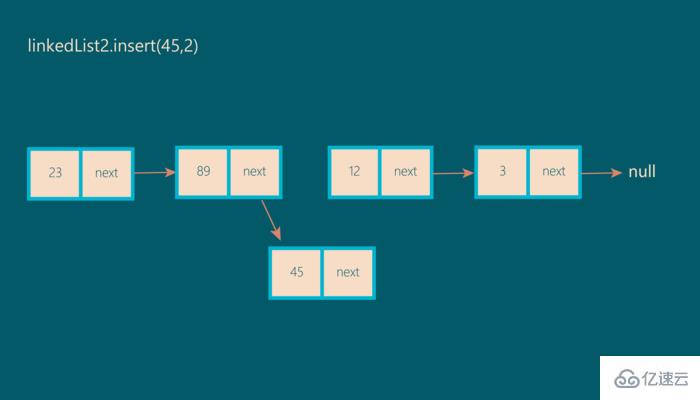
第3步：

將新節點(45)的 next 指向給下一個節點(12)

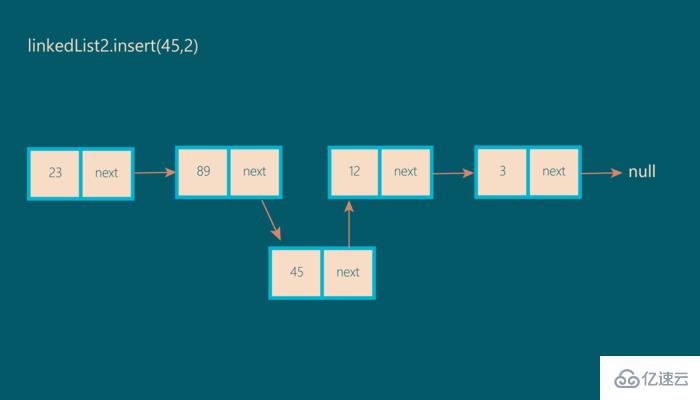
這就是執行插入操作的方式。 通過以上可視化，我們觀察到需要在index-1位置和index位置找到節點，以便可以在它們之間插入新節點。 在代碼中實現：

insert (value, index) {
  if (index >= this.length) {
  this.append(value)
}

  const node = new Node(value)

  const { prevNode, nextNode } = thisg.getPrevNextNodes(index)
  prevNode.next = node
  node.next = nextNode

  this.length++
}

簡單分析一下上面的函數：

如果index的值大于或等于length屬性，則將操作移交給append函數。 對于 else 分支，我們使用 Node 類創建一個新節點，接下來觀察一個新函數getPrevNextNodes() ，通過該函數我們可以接收prevNode和nextNode的值。 getPrevNextNodes函數的實現如下：

 getPrevNextNodes(index){
    let count = 0;
    let prevNode = this.head;
    let nextNode = prevNode.next;

    while(count < index - 1){
      prevNode = prevNode.next;
      nextNode = prevNode.next;
      count++;
    }

    return {
      prevNode,
      nextNode
    }
  }

通過遍歷鏈表返回在index-1位置和index位置的節點，并將prevNode的next屬性指向新節點，并將新節點的next屬性指向nextNode。

鏈表的插入操作的復雜度為 O(n)，因為我們必須遍歷鏈表并在index-1和 index 位置搜索節點。 盡管復雜度為O(n)，但我們發現此插入操作比對數組的插入操作快得多，在數組中，我們必須將所有元素的索引移到特定索引之后，但是在鏈接中，我們僅操縱 index-1 和index 位置的節點的下一個屬性。

remove (刪除特定索引處的元素)

實現了插入操作之后，刪除操作就比較容易理解，因為它幾乎與插入操作相同，當我們從getPrevNextNodes函數獲取prevNode和nextNode值時，我們必須在remove中執行以下操作：

remove(index){
  let {previousNode,currentNode} = this.getNodes(index)
  previousNode.next = currentNode.next
  this.length--
}

刪除操作的復雜度也為 O(n)，類似于插入操作，鏈表中的刪除操作比數組中的刪除操作要快。

reverse (反轉鏈表)

雖然看起來很簡單，但反轉鏈表常常是實現起來最令人困惑的操作，因此，在面試中會經常詢問這個操作。在實現這個函數之前，讓我們先把反轉鏈表的策略可視化一下。

為了反轉鏈表，我們需要跟蹤三個節點，previousNode，currentNode和nextNode。

考慮下面的鏈表:

let linkedList2 = new LinkedList()
linkedList2.append(67)
linkedList2.append(32)
linkedList2.append(44)

第一步：

開始，previousNode的值為null，而currentNode的值為head：

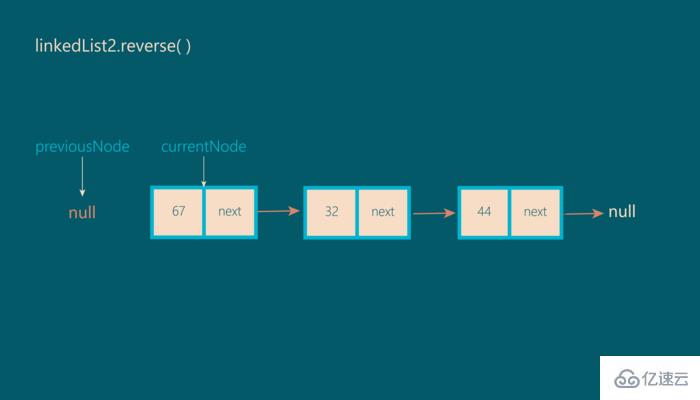
第二步：

接下來，我們將nextNode分配給currentNode.next：

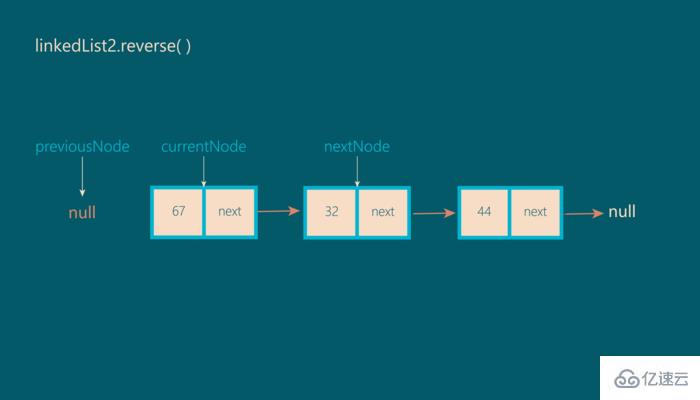
第三步：

接下來，我們將currentNode.next屬性指向previousNode：

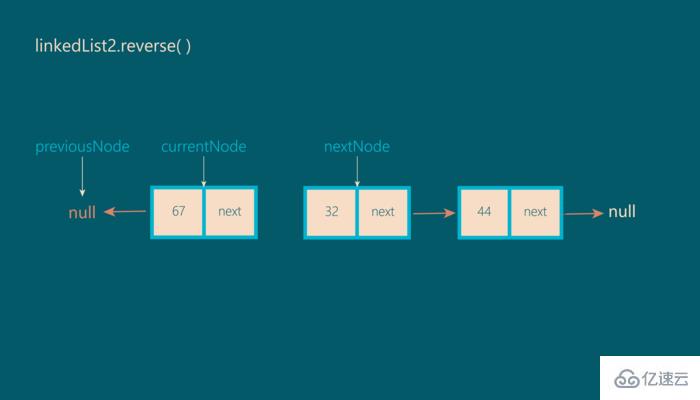
第三步：

現在，我們將previousNode移至currentNode，將currentNode移至nextNode：

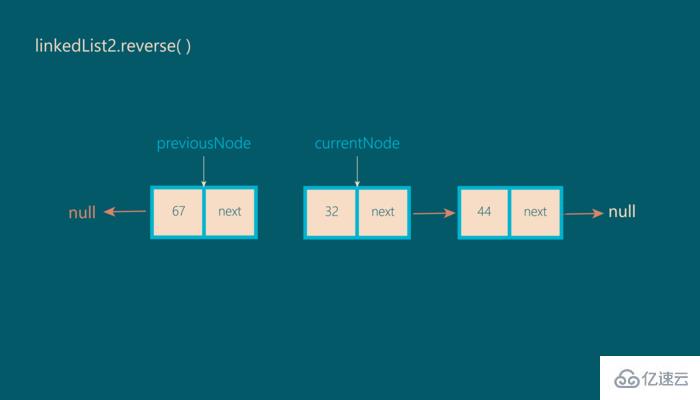
這個過程從步驟2重復操作，一直到currentNode 等于 null。

reverse (){
  let previousNode = null
  let currentNode = this.head

  while(currentNode !== null) {
    let nextNode = currentNode.next
    currentNode.next = previousNode
    previousNode = currentNode
    currentNode = nextNode
  }

  this.head = previousNode
}

就像我們看到的一樣，直到currentNode === null，我們一直在遍歷和移動這些值。 最后，我們將previousNode值分配給head。

反向運算的復雜度為O(n)。

查找 (查找特定索引的值)

這個操作很簡單，我們只是遍歷鏈表并返回特定索引處的節點。這個操作的復雜度也是O(n)。

lookup(index){
    let counter = 0;
    let currentNode = this.head;
    while(counter < index){
      currentNode = currentNode.next;
      counter++;
    }
    return currentNode;
  }

好了，我們已經完成了用javascript實現單個鏈表的基本操作。單鏈表和雙鏈表的區別在于，雙鏈表的節點具有指向前一個節點和下一個節點的指針。

鏈表為我們提供了快速的append（末尾添加元素）和prepend（開頭添加元素）操作。 盡管鏈表中的插入操作的復雜度為O(n)，但比數組的插入操作要快得多。 使用數組時我們面臨的另一個問題是大小復雜性，當使用動態數組時，在添加元素時，我們必須將整個數組復制到另一個地址空間，然后添加元素，而在鏈表中，我們不需要 面對這樣的問題。

在使用對象時，我們面臨的問題是元素在內存中的隨機位置，而在鏈表中，節點是通過指針相互連接的，指針提供了一定的順序。

感謝各位的閱讀！關于“JS數據結構之鏈表的優點是什么”這篇文章就分享到這里了，希望以上內容可以對大家有一定的幫助，讓大家可以學到更多知識，如果覺得文章不錯，可以把它分享出去讓更多的人看到吧！