怎么在python中利用matplotlib創建一個三維圖表

本篇文章為大家展示了怎么在python中利用matplotlib創建一個三維圖表，內容簡明扼要并且容易理解，絕對能使你眼前一亮，通過這篇文章的詳細介紹希望你能有所收獲。

 Matplotlib 自動安裝：

from mpl_toolkits import mplot3d

一旦模塊被導入，三維 axes 就可以像其他普通 axes 一樣通過關鍵字參數projection='3d'來創建：

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure()
ax = plt.axes(projection='3d')
plt.show()

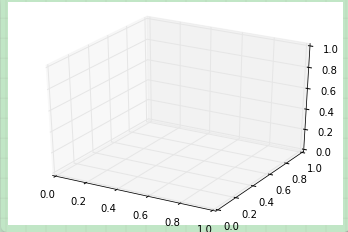
三維 axes 激活后，我們可以在上面繪制不同的三維圖表類型。三維圖表在 notebook 中使用交互式圖表展示會優于使用靜態展示；回憶我們前面介紹過，你可以使用%matplotlib notebook而不是%matplotlib inline來激活交互式展示模式。

三維的點和線

三維圖表中最基礎的是使用(x, y, z)坐標定義的一根線或散點的集合。前面介紹過普通的二維圖表，作為類比，使用ax.plot3D和ax.scatter3D函數可以創建三維折線和散點圖。這兩個函數的簽名與二維的版本基本一致，你可以參考[簡單折線圖]和[簡單散點圖]來復習一下這部分的內容。下面我們繪制一個三維中的三角螺旋，在線的附近在繪制一些隨機的點：

ax = plt.axes(projection='3d')

# 三維螺旋線的數據
zline = np.linspace(0, 15, 1000)
xline = np.sin(zline)
yline = np.cos(zline)
ax.plot3D(xline, yline, zline, 'gray')

# 三維散點的數據
zdata = 15 * np.random.random(100)
xdata = np.sin(zdata) + 0.1 * np.random.randn(100)
ydata = np.cos(zdata) + 0.1 * np.random.randn(100)
ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='Greens');

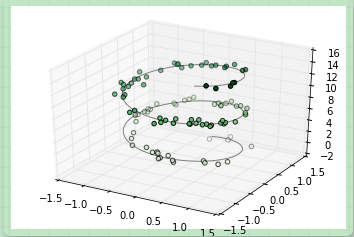
注意默認情況下，圖中的散點會有透明度的區別，用于體現在圖中散點的深度。雖然三維效果在靜態圖像中難以顯示，你可以使用交互式的視圖來獲得更佳的三維直觀效果。

三維輪廓圖

類似于我們在[密度和輪廓圖]中介紹的內容，mplot3d也包含著能夠創建三維浮雕圖像的工具。就像二維的ax.contour圖表，ax.contour3D要求輸入數據的格式是二維普通網格上計算得到的 Z 軸的數據值。下面我們展示一個三維的正弦函數輪廓圖：

def f(x, y):
  return np.sin(np.sqrt(x ** 2 + y ** 2))

x = np.linspace(-6, 6, 30)
y = np.linspace(-6, 6, 30)

X, Y = np.meshgrid(x, y)
Z = f(X, Y)

fig = plt.figure()
ax = plt.axes(projection='3d')
ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z');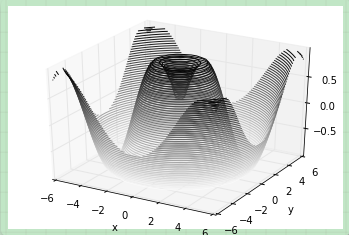

有時候默認的視角角度不是最理想的，在這種情況下我們可以使用view_init函數來設置水平角和方位角。在下面的例子中，我們使用的是 60° 的水平角（即以 60° 俯視 x-y 平面）和 35° 的方位角（即將 z 軸逆時針旋轉 35°）：

ax.view_init(60, 35)
fig

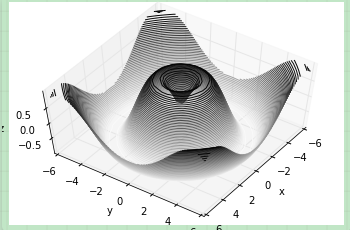
同樣，注意到當使用 Matplotlib 交互式展示是，這樣的旋轉可以通過鼠標點擊和拖拽來實現。

框線圖和表面圖

使用網格數據生成的三維圖表還有框線圖和表面圖。這兩種圖表將網格數據投射到特定的三維表面，能夠使得結果圖像非常直觀和具有說服力。下面是一個框線圖的例子：

fig = plt.figure()
ax = plt.axes(projection='3d')
ax.plot_wireframe(X, Y, Z, color='black')
ax.set_title('wireframe');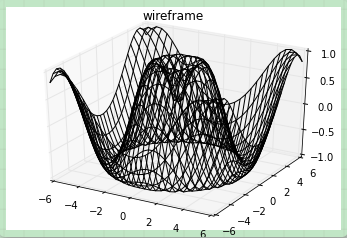

表面圖類似框線圖，區別在于每個框線構成的多邊形都使用顏色進行了填充。添加色圖用于填充多邊形能夠讓圖形表面展示出來：

ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
        cmap='viridis', edgecolor='none')
ax.set_title('surface');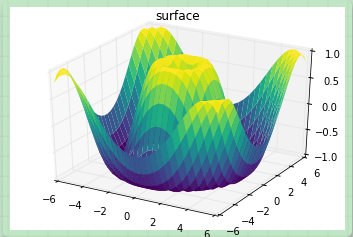

注意雖然每個顏色填充的表面都是二維的，但是表面的邊緣不需要是直線構成的。下面的例子使用surface3D繪制了一個部分極坐標網格，能夠讓我們切入到函數內部觀察效果：

r = np.linspace(0, 6, 20)
theta = np.linspace(-0.9 * np.pi, 0.8 * np.pi, 40)
r, theta = np.meshgrid(r, theta)

X = r * np.sin(theta)
Y = r * np.cos(theta)
Z = f(X, Y)

ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
        cmap='viridis', edgecolor='none');

表面三角剖分

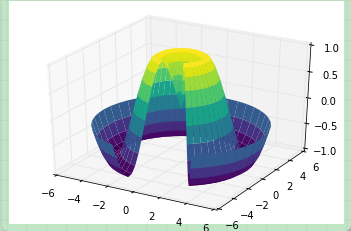
在一些應用場合中，上面的這種均勻網格繪制的圖表方式太過于局限和不方便。在這些情況下，三角剖分的圖表可以派上用場。如果我們并不是使用笛卡爾坐標系或極坐標系的網格來繪制三維圖表，而是使用一組隨機的點來繪制三維圖表呢？

theta = 2 * np.pi * np.random.random(1000)
r = 6 * np.random.random(1000)
x = np.ravel(r * np.sin(theta))
y = np.ravel(r * np.cos(theta))
z = f(x, y)

ax = plt.axes(projection='3d')
ax.scatter(x, y, z, c=z, cmap='viridis', linewidth=0.5);

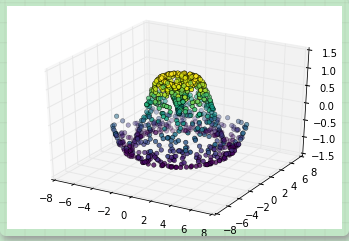
上圖并未形象的表示出表面情況。這種情況下我們可以使用ax.plot_trisurf函數，它能首先根據我們的數據輸入找到各點內在的三角函數形式，然后繪制表面（注意的是這里的 x，y，z 是一維的數組）：

ax = plt.axes(projection='3d')
ax.plot_trisurf(x, y, z,
        cmap='viridis', edgecolor='none');

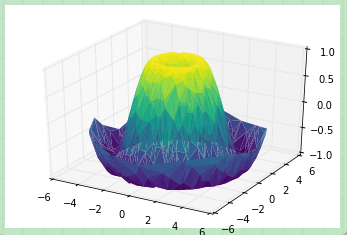
上圖的結果很顯然沒有使用網格繪制表面圖那么清晰，但是對于我們并不是使用函數構建數據樣本（數據樣本通常來自真實世界的采樣）的情況下，這能提供很大的幫助。例如我們下面會看到，能使用這種方法繪制一條三維的莫比烏斯環。

例子：繪制莫比烏斯環

theta = np.linspace(0, 2 * np.pi, 30)
w = np.linspace(-0.25, 0.25, 8)
w, theta = np.meshgrid(w, theta)

phi = 0.5 * theta

現在我們已經有了所有需要獲得三維坐標值的參數了。我們定義  為每個坐標點距離環形中間的位置，使用它來計算最終(x,y,z)  三維坐標系的坐標值：

# r是坐標點距離環形中心的距離值
r = 1 + w * np.cos(phi)
# 利用簡單的三角函數知識算得x，y，z坐標值
x = np.ravel(r * np.cos(theta))
y = np.ravel(r * np.sin(theta))
z = np.ravel(w * np.sin(phi))

最后，為了繪制對象，我們必須保證三角剖分是正確的。實現這個最好的方法是在底層的參數上面實現三角剖分，最后讓 Matplotlib 將這個三角剖分投射到三維空間中形成莫比烏斯環。下面的代碼最終繪制圖形：

# 在底層參數的基礎上進行三角剖分
from matplotlib.tri import Triangulation
tri = Triangulation(np.ravel(w), np.ravel(theta))

ax = plt.axes(projection='3d')
ax.plot_trisurf(x, y, z, triangles=tri.triangles,
        cmap='viridis', linewidths=0.2);

ax.set_xlim(-1, 1); ax.set_ylim(-1, 1); ax.set_zlim(-1, 1);

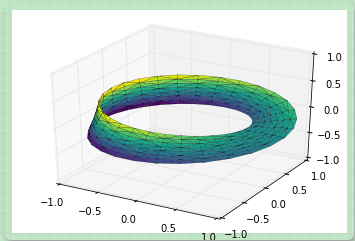
上述內容就是怎么在python中利用matplotlib創建一個三維圖表，你們學到知識或技能了嗎？如果還想學到更多技能或者豐富自己的知識儲備，歡迎關注億速云行業資訊頻道。