從零開始利用Python建立邏輯回歸分類模型

假設申請人向你提供成績，你根據成績對其進行分類，目標是根據分數將申請人分為兩類，如果申請人可以進入大學，則分為1級，如果申請人不能被錄取，則分為0級。使用線性回歸可以解決這個問題嗎？讓我們一起來看看。

注意：閱讀本文的前提是了解線性回歸！

目錄

• 什么是邏輯回歸？

• 數據集可視化

• 假設和成本函數

• 從頭開始訓練模型

• 模型評估

• Scikit-learn實現

什么是邏輯回歸？

回想一下線性回歸，它被用于確定一個連續因變量的值。邏輯回歸通常用于分類目的。與線性回歸不同，因變量只能采用有限數量的值，即因變量是分類的。當可能結果的數量只有兩個時，它被稱為二元邏輯回歸。

讓我們看看邏輯回歸如何被用于分類任務。

在線性回歸中，輸出是輸入的加權和。邏輯回歸是廣義線性回歸，在某種意義上，我們不直接輸出輸入的加權和，但我們通過一個函數來傳遞它，該函數可以映射0到1之間的任何實數值。

如果我們將輸入的加權和作為輸出，就像我們在線性回歸中做的那樣，那么該值可以大于1，但我們想要一個介于0和1之間的值。這也是為什么線性回歸不能用于分類任務的原因。

從下圖可以看出，線性回歸的輸出通過一個激活函數傳遞，該函數可以映射0到1之間的任何實數值。

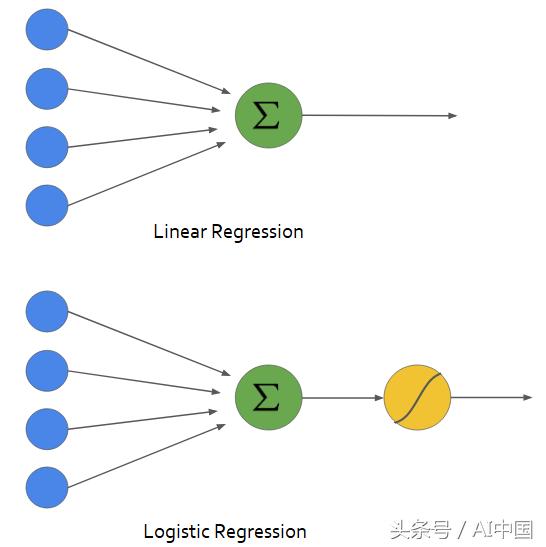
所使用的激活函數稱為sigmoid函數。sigmoid函數的曲線如下圖所示

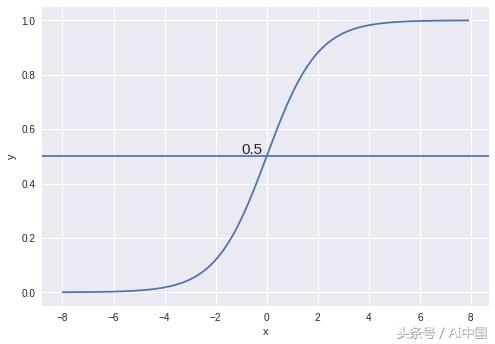
我們可以看到sigmoid函數的值總是介于0和1之間。在X = 0時，該值恰好為0.5。我們可以使用0.5作為概率閾值來確定類。如果概率大于0.5，我們將其分類為Class-1（Y = 1）或者歸類為Class-0（Y = 0）。

在我們構建模型之前，讓我們看一下邏輯回歸所做的假設

• 因變量必須是絕對的

• 自變量（特征）必須是獨立的（以避免多重共線性）

數據集

本文中使用的數據來自吳恩達在Coursera上的機器學習課程。數據可以從這里下載。（https://www.coursera.org/learn/machine-learning）該數據包括100名申請人的兩次考試分數。目標值采用二進制值1,0。1表示申請人被大學錄取，0表示申請人未被錄取。它目標是建立一個分類器，可以預測申請是否將被大學錄取。

讓我們使用read_csv函數將數據加載到pandas Dataframe中。我們還將數據分為錄取的和未錄取的，以使數據可視化。

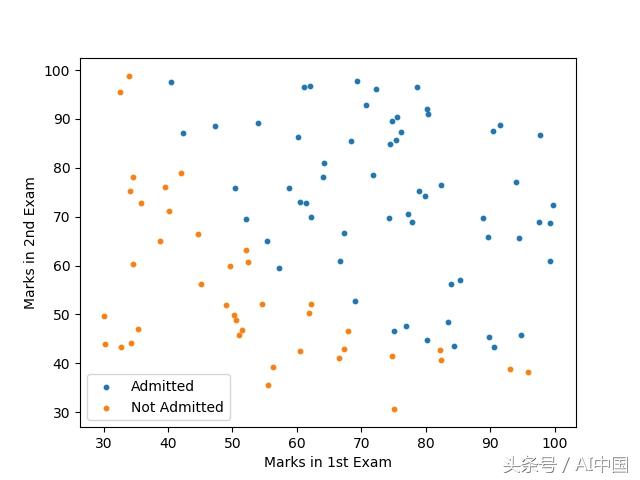
現在我們已經清楚地了解了問題和數據，讓我們繼續構建我們的模型。

假設和成本函數

到目前為止，我們已經了解了如何使用邏輯回歸將實例分類到不同的類中。在本節中，我們將定義假設和成本函數。

線性回歸模型可以用等式表示。

然后，我們將sigmoid函數應用于線性回歸的輸出

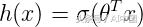
sigmoid函數表示為，

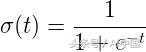
然后邏輯回歸的假設為，

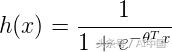
如果輸入的加權和大于零，則預測的類為1，反之亦然。因此，通過將輸入的加權和設置為0，可以找到將兩個類分開的決策邊界。

成本函數

與線性回歸一樣，我們將為模型定義成本函數，目標是最小化成本。

單個訓練示例的成本函數可以通過以下方式給出：

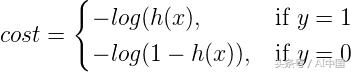
成本函數直覺

如果實際的類是1并且模型預測為0，我們應該懲罰它，反之亦然。從下圖中可以看出，對于h（x）接近1的情況-log（h（x）），成本為0，當h（x）接近0時，成本為無窮大（即我們對模型進行嚴重懲罰）。類似地，對于繪圖-log（1-h（x）），當實際值為0并且模型預測為0時，成本為0并且當h（x）接近1時成本變為無窮大。

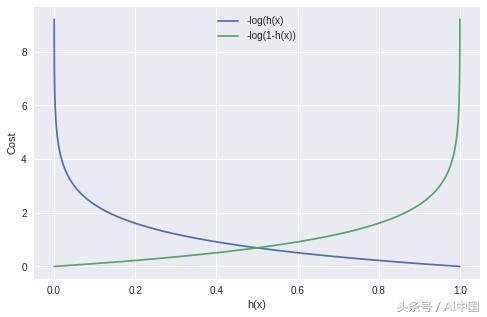
我們可以使用以下兩個方程組合：

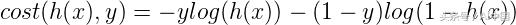
由J（θ）表示的所有訓練樣本的成本可以通過取所有訓練樣本的成本的平均值來計算

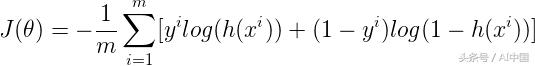
其中m是訓練樣本的數量。

我們將使用梯度下降來最小化成本函數。梯度w.r.t任何參數都可以由該方程給出

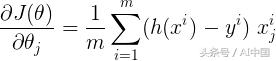
該方程類似于我們在線性回歸中所獲得的方程，在這兩種情況下只有h（x）不同。

訓練模型

現在我們已經擁有了構建模型所需的一切。讓我們在代碼中實現它。

讓我們首先為我們的模型準備數據。

我們將定義一些將用于計算成本的函數。

接下來，我們定義成本和梯度函數。

我們還定義擬合函數，該函數將用于查找最小化成本函數的模型參數。在這篇文章中，我們編寫了梯度下降法來計算模型參數。 在這里，我們將使用scipy庫中的fmin_tnc函數。它可用于計算任何函數的最小值。它將參數作為：

• func：最小化的函數

• x0：我們想要查找的參數的初始值

• fprime：'func'定義的函數的梯度

• args：需要傳遞給函數的參數

模型參數為[-25.16131856 0.20623159 0.20147149]

為了了解我們的模型有多好，我們將繪制決策邊界。

繪制決策邊界

由于我們的數據集中有兩個特征，因此線性方程可以表示為，

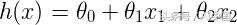
如前所述，可以通過將輸入的加權和設置為0來找到決策邊界。將h（x）等于0，

我們將在我們用于可視化數據集的圖上方繪制決策邊界。

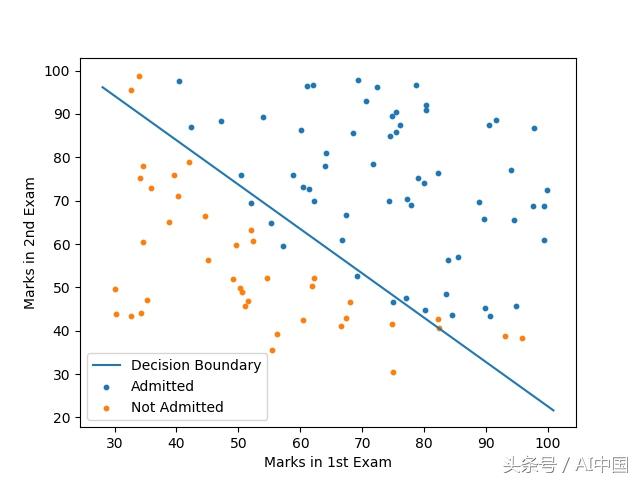
看起來我們的模型在預測課程方面做得不錯。但它有多準確？讓我們來看看。

模型的準確性

該模型的準確率為89％。

讓我們使用scikit-learn實現我們的分類器，并將它與我們從頭開始構建的模型進行比較。

scikit-learn實現

模型參數為[[-2.85831439,0.05214733,0.04531467]]，精度為91％。

為什么模型參數與我們從頭開始實現的模型有很大不同？如果你看一下sk-learn的邏輯回歸實現的文檔，你就會發現其中考慮了正則化。基本上，正則化是用于防止模型過度擬合數據的。 在本文中，我不會深入討論正規化的細節。

此文章中使用的完整代碼可以在此GitHub中找到。（https://github.com/animesh-agarwal/Machine-Learning/tree/master/LogisticRegression）