您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本文實例講述了Java基于動態規劃法實現求最長公共子序列及最長公共子字符串。分享給大家供大家參考,具體如下:
動態規劃法
經常會遇到復雜問題不能簡單地分解成幾個子問題,而會分解出一系列的子問題。簡單地采用把大問題分解成子問題,并綜合子問題的解導出大問題的解的方法,問題求解耗時會按問題規模呈冪級數增加。
為了節約重復求相同子問題的時間,引入一個數組,不管它們是否對最終解有用,把所有子問題的解存于該數組中,這就是動態規劃法所采用的基本方法。
【問題】 求兩字符序列的最長公共字符子序列
問題描述:字符序列的子序列是指從給定字符序列中隨意地(不一定連續)去掉若干個字符(可能一個也不去掉)后所形成的字符序列。令給定的字符序列X=“x0,x1,…,xm-1”,序列Y=“y0,y1,…,yk-1”是X的子序列,存在X的一個嚴格遞增下標序列<i0,i1,…,ik-1>,使得對所有的j=0,1,…,k-1,有xij=yj。例如,X=“ABCBDAB”,Y=“BCDB”是X的一個子序列。
考慮最長公共子序列問題如何分解成子問題,設A=“a0,a1,…,am-1”,B=“b0,b1,…,bm-1”,并Z=“z0,z1,…,zk-1”為它們的最長公共子序列。不難證明有以下性質:
(1) 如果am-1=bn-1,則zk-1=am-1=bn-1,且“z0,z1,…,zk-2”是“a0,a1,…,am-2”和“b0,b1,…,bn-2”的一個最長公共子序列;
(2) 如果am-1!=bn-1,則若zk-1!=am-1,蘊涵“z0,z1,…,zk-1”是“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一個最長公共子序列;
(3) 如果am-1!=bn-1,則若zk-1!=bn-1,蘊涵“z0,z1,…,zk-1”是“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一個最長公共子序列。
這樣,在找A和B的公共子序列時,如有am-1=bn-1,則進一步解決一個子問題,找“a0,a1,…,am-2”和“b0,b1,…,bm-2”的一個最長公共子序列;如果am-1!=bn-1,則要解決兩個子問題,找出“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一個最長公共子序列和找出“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一個最長公共子序列,再取兩者中較長者作為A和B的最長公共子序列。
求解:
引進一個二維數組c[][],用c[i][j]記錄X[i]與Y[j] 的LCS 的長度,b[i][j]記錄c[i][j]是通過哪一個子問題的值求得的,以決定搜索的方向。
我們是自底向上進行遞推計算,那么在計算c[i,j]之前,c[i-1][j-1],c[i-1][j]與c[i][j-1]均已計算出來。此時我們根據X[i] = Y[j]還是X[i] != Y[j],就可以計算出c[i][j]。
問題的遞歸式寫成:
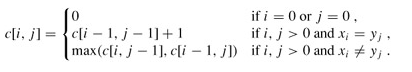
回溯輸出最長公共子序列過程:
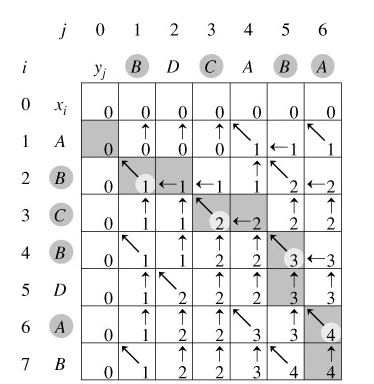
算法分析:
由于每次調用至少向上或向左(或向上向左同時)移動一步,故最多調用(m * n)次就會遇到i = 0或j = 0的情況,此時開始返回。返回時與遞歸調用時方向相反,步數相同,故算法時間復雜度為Θ(m * n)。
Java代碼實現:
public class LCSProblem
{
public static void main(String[] args)
{
//保留空字符串是為了getLength()方法的完整性也可以不保留
//但是在getLength()方法里面必須額外的初始化c[][]第一個行第一列
String[] x = {"", "A", "B", "C", "B", "D", "A", "B"};
String[] y = {"", "B", "D", "C", "A", "B", "A"};
int[][] b = getLength(x, y);
Display(b, x, x.length-1, y.length-1);
}
/**
* @param x
* @param y
* @return 返回一個記錄決定搜索的方向的數組
*/
public static int[][] getLength(String[] x, String[] y)
{
int[][] b = new int[x.length][y.length];
int[][] c = new int[x.length][y.length];
for(int i=1; i<x.length; i++)
{
for(int j=1; j<y.length; j++)
{
//對應第一個性質
if( x[i] == y[j])
{
c[i][j] = c[i-1][j-1] + 1;
b[i][j] = 1;
}
//對應第二或者第三個性質
else if(c[i-1][j] >= c[i][j-1])
{
c[i][j] = c[i-1][j];
b[i][j] = 0;
}
//對應第二或者第三個性質
else
{
c[i][j] = c[i][j-1];
b[i][j] = -1;
}
}
}
return b;
}
//回溯的基本實現,采取遞歸的方式
public static void Display(int[][] b, String[] x, int i, int j)
{
if(i == 0 || j == 0)
return;
if(b[i][j] == 1)
{
Display(b, x, i-1, j-1);
System.out.print(x[i] + " ");
}
else if(b[i][j] == 0)
{
Display(b, x, i-1, j);
}
else if(b[i][j] == -1)
{
Display(b, x, i, j-1);
}
}
}
運行結果:
B C B A
最長公共子字符串:類似最長子序列,只是公共子字符串要求必須是連續的。
java實現代碼如下:
public class stringCompare {
//在動態規劃矩陣生成方式當中,每生成一行,前面的那一行就已經沒有用了,因此這里只需使用一維數組,而不是常用的二位數組
public static void getLCString(char[] str1, char[] str2) {
int len1, len2;
len1 = str1.length;
len2 = str2.length;
int maxLen = len1 > len2 ? len1 : len2;
int[] max = new int[maxLen];// 保存最長子串長度的數組
int[] maxIndex = new int[maxLen];// 保存最長子串長度最大索引的數組
int[] c = new int[maxLen];
int i, j;
for (i = 0; i < len2; i++) {
for (j = len1 - 1; j >= 0; j--) {
if (str2[i] == str1[j]) {
if ((i == 0) || (j == 0))
c[j] = 1;
else
c[j] = c[j - 1] + 1;//此時C[j-1]還是上次循環中的值,因為還沒被重新賦值
} else {
c[j] = 0;
}
// 如果是大于那暫時只有一個是最長的,而且要把后面的清0;
if (c[j] > max[0]) {
max[0] = c[j];
maxIndex[0] = j;
for (int k = 1; k < maxLen; k++) {
max[k] = 0;
maxIndex[k] = 0;
}
}
// 有多個是相同長度的子串
else if (c[j] == max[0]) {
for (int k = 1; k < maxLen; k++) {
if (max[k] == 0) {
max[k] = c[j];
maxIndex[k] = j;
break; // 在后面加一個就要退出循環了
}
}
}
}
for (int temp : c) {
System.out.print(temp);
}
System.out.println();
}
//打印最長子字符串
for (j = 0; j < maxLen; j++) {
if (max[j] > 0) {
System.out.println("第" + (j + 1) + "個公共子串:");
for (i = maxIndex[j] - max[j] + 1; i <= maxIndex[j]; i++)
System.out.print(str1[i]);
System.out.println(" ");
}
}
}
public static void main(String[] args) {
String str1 = new String("binghaven");
String str2 = new String("jingseven");
getLCString(str1.toCharArray(), str2.toCharArray());
}
}
輸出:
000000000
010000000
002000001
000300000
000000000
000000010
000000100
000000020
001000003
第1個公共子串:
ing
第2個公共子串:
ven
更多關于java算法相關內容感興趣的讀者可查看本站專題:《Java數據結構與算法教程》、《Java操作DOM節點技巧總結》、《Java文件與目錄操作技巧匯總》和《Java緩存操作技巧匯總》
希望本文所述對大家java程序設計有所幫助。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。