編程語言中如何通過先序遍歷和中序遍歷后的序列還原二叉樹

小編給大家分享一下編程語言中如何通過先序遍歷和中序遍歷后的序列還原二叉樹，希望大家閱讀完這篇文章之后都有所收獲，下面讓我們一起去探討吧！

當我們有一個

先序遍歷序列：1,3,7,9,5,11

中序遍歷序列：9,7,3,1,5,11

我們可以很輕松的用筆寫出對應的二叉樹。但是用代碼又該如何實現？

下面我們來簡單談談基本思想。

首先，先序遍歷的順序是根據 根-左孩子-右孩子 的順序遍歷的，那么我們可以率先確認的是先序遍歷序列的第一個數就是根節點，然后中序遍歷是根據 左孩子-根-右孩子 的順序遍歷的。我們通過先序遍歷確認了根節點，那么我們只需要在中序遍歷中找到根節點的位置，然后就可以很好地區分出，那些屬于左子樹的節點，那些是屬于右子樹的節點了。如下圖：

我們確定數字1為根節點，然后根據中序遍歷的遍歷順序確定，中序遍歷序列中數字1的左邊全部為左子樹節點，右邊全部為右子樹。通過左子樹節點的個數，得出先序遍歷序列中從根節點往后的連續3個數是屬于左子樹的，剩下的為右子樹。這樣再在左右子樹的序列中重復以上步驟，最終找到沒有子節點為止。

實現代碼如下：

package com.tree.traverse;

import java.util.ArrayList;
import java.util.List;

/**
 * @author Caijh
 *
 * 2017年6月2日 下午7:21:10
 */

public class BuildTreePreOrderInOrder {

  /** 
   *       1 
   *       / \
   *      3  5 
   *      /   \
   *     7    11
   *    / 
   *   9    
   */ 
  public static int treeNode = 0;//記錄先序遍歷節點的個數
  private List<Node> nodeList = new ArrayList<>();//層次遍歷節點的隊列
  public static void main(String[] args) {
    BuildTreePreOrderInOrder build = new BuildTreePreOrderInOrder();
    int[] preOrder = { 1, 3, 7, 9, 5, 11};
    int[] inOrder = { 9, 7, 3, 1, 5, 11};
    
    treeNode = preOrder.length;//初始化二叉樹的節點數
    Node root = build.buildTreePreOrderInOrder(preOrder, 0, preOrder.length - 1, inOrder, 0, preOrder.length - 1);
    System.out.print("先序遍歷：");
    build.preOrder(root);
    System.out.print("\n中序遍歷：");
    build.inOrder(root);
    System.out.print("\n原二叉樹：\n");
    build.prototypeTree(root);
  }

  /**
   * 分治法
   * 通過先序遍歷結果和中序遍歷結果還原二叉樹
   * @param preOrder  先序遍歷結果序列
   * @param preOrderBegin   先序遍歷起始位置下標
   * @param preOrderEnd  先序遍歷末尾位置下標
   * @param inOrder  中序遍歷結果序列
   * @param inOrderBegin  中序遍歷起始位置下標
   * @param inOrderEnd   中序遍歷末尾位置下標
   * @return
   */
  public Node buildTreePreOrderInOrder(int[] preOrder, int preOrderBegin, int preOrderEnd, int[] inOrder, int inOrderBegin, int inOrderEnd) {
    if (preOrderBegin > preOrderEnd || inOrderBegin > inOrderEnd) {
      return null;
    }
    int rootData = preOrder[preOrderBegin];//先序遍歷的第一個字符為當前序列根節點
    Node head = new Node(rootData);
    int divider = findIndexInArray(inOrder, rootData, inOrderBegin, inOrderEnd);//找打中序遍歷結果集中根節點的位置
    int offSet = divider - inOrderBegin - 1;//計算左子樹共有幾個節點，節點數減一，為數組偏移量
    Node left = buildTreePreOrderInOrder(preOrder, preOrderBegin + 1, preOrderBegin + 1 + offSet, inOrder, inOrderBegin,inOrderBegin + offSet);
    Node right = buildTreePreOrderInOrder(preOrder, preOrderBegin + offSet + 2, preOrderEnd, inOrder, divider + 1, inOrderEnd);
    head.left = left;
    head.right = right;
    return head;
  }
  /**
   * 通過先序遍歷找到的rootData根節點，在中序遍歷結果中區分出：中左子樹和右子樹
   * @param inOrder  中序遍歷的結果數組
   * @param rootData  根節點位置
   * @param begin  中序遍歷結果數組起始位置下標
   * @param end  中序遍歷結果數組末尾位置下標
   * @return return中序遍歷結果數組中根節點的位置
   */
  public int findIndexInArray(int[] inOrder, int rootData, int begin, int end) {
    for (int i = begin; i <= end; i++) {
      if (inOrder[i] == rootData)
        return i;
    }
    return -1;
  }
  /**
   * 二叉樹先序遍歷結果
   * @param n
   */
  public void preOrder(Node n) {
    if (n != null) {
      System.out.print(n.val + ",");
      preOrder(n.left);
      preOrder(n.right);
    }
  }
  /**
   * 二叉樹中序遍歷結果
   * @param n
   */
  public void inOrder(Node n) {
    if (n != null) {
      inOrder(n.left);
      System.out.print(n.val + ",");
      inOrder(n.right);
    }
  }
  /**
   * 還原后的二叉樹
   * 二叉數層次遍歷
   * 基本思想：
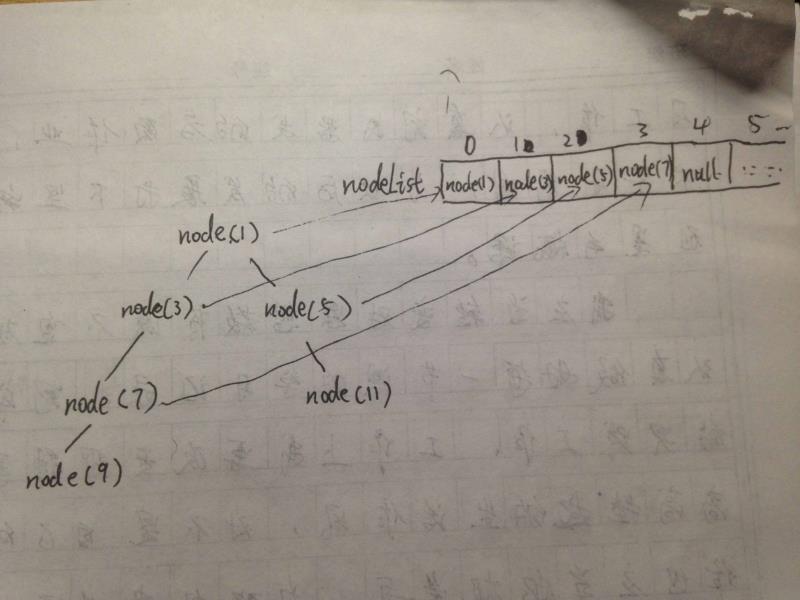
   *   1.因為推導出來的二叉樹是保存在Node類對象的子對象里面的，（類似于c語言的結構體）如果通過遞歸實現層次遍歷的話，不容易實現
   *   2.這里采用List隊列逐層保存Node對象節點的方式實現對二叉樹的層次遍歷輸出
   *   3.如果父節點的位置為i,那么子節點的位置為，2i 和 2i+1;依據這個規律逐層遍歷，通過保存的父節點，找到子節點。并保存，不斷向下遍歷保存。
   * @param tree
   */
  public void prototypeTree(Node tree){
    //用list存儲層次遍歷的節點
    if(tree !=null){
      if(tree!=null)
        nodeList.add(tree);
      nodeList.add(tree.left);
      nodeList.add(tree.right);
      int count=3;
      //從第三層開始
      for(int i=3;count<treeNode;i++){
        //第i層第一個子節點的父節點的位置下標
        int index = (int) Math.pow(2, i-1-1)-1;
        /**
         * 二叉樹的每一層節點數遍歷
         * 因為第i層的最大節點數為2的i-1次方個，
         */
        for(int j=1;j<=Math.pow(2, i-1);){
          //計算有效的節點的個數，和遍歷序列的總數做比較，作為判斷循環結束的標志
          if(nodeList.get(index).left!=null)
            count++;
          if(nodeList.get(index).right!=null)
            count++;
          nodeList.add(nodeList.get(index).left);
          nodeList.add(nodeList.get(index).right);
          index++;
          if(count>=treeNode)//當所有有效節點都遍歷到了就結束遍歷
            break;
          j+=2;//每次存儲兩個子節點，所以每次加2
        }
      }
      int flag=0,floor=1;
      for(Node node:nodeList){
        if(node!=null)
          System.out.print(node.val+" ");
        else
          System.out.print("# ");//#號表示空節點
        flag++;
        /**
         * 逐層遍歷輸出二叉樹
         * 
         */
        if(flag>=Math.pow(2, floor-1)){
          flag=0;
          floor++;
          System.out.println();
        }
      }
    }
  }
  /**
   * 內部類
   * 1.每個Node類對象為一個節點，
   * 2.每個節點包含根節點，左子節點和右子節點
   */
  class Node {
    Node left;
    Node right;
    int val;
    public Node(int val) {
      this.val = val;
    }
  }
}

運行結果：

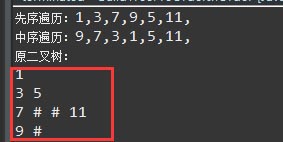
最后逐層輸出二叉樹的基本思想：

* 1.因為推導出來的二叉樹是保存在Node類對象的子對象里面的，（類似于c語言的結構體）如果通過遞歸實現層次遍歷的話，不容易實現

* 2.這里采用List隊列逐層保存Node對象節點的方式實現對二叉樹的層次遍歷輸出

* 3.如果父節點的位置為i,那么子節點的位置為，2i 和 2i+1;依據這個規律逐層遍歷，通過保存的父節點，找到子節點。并保存，不斷向下遍歷保存。

看完了這篇文章，相信你對“編程語言中如何通過先序遍歷和中序遍歷后的序列還原二叉樹”有了一定的了解，如果想了解更多相關知識，歡迎關注億速云行業資訊頻道，感謝各位的閱讀！