C語言中怎么實現一個平衡二叉樹

這篇文章將為大家詳細講解有關C語言中怎么實現一個平衡二叉樹，文章內容質量較高，因此小編分享給大家做個參考，希望大家閱讀完這篇文章后對相關知識有一定的了解。

數據結構平衡二叉樹

參考代碼如下：

#include <stdio.h> 
#include <malloc.h> 
#include <windows.h> 
#define LH +1  // 左高  
#define EH 0  // 等高  
#define RH -1  // 右高  
#define N 5   // 數據元素個數  
 
typedef char KeyType; // 設關鍵字域為字符型  
 
typedef struct 
{ 
  KeyType key; 
  int order; 
}ElemType; // 數據元素類型  
 
// 平衡二叉樹的類型  
typedef struct BSTNode 
{ 
  ElemType data; 
  // bf結點的平衡因子,只能夠取0，-1，1，它是左子樹的深度減去 
  // 右子樹的深度得到的 
  int bf;  
  struct BSTNode *lchild,*rchild; // 左、右孩子指針  
}BSTNode,*BSTree; 
 
// 構造一個空的動態查找表DT 
int InitDSTable(BSTree *DT)  
{ 
  *DT=NULL; 
  return 1; 
} 
 
// 銷毀動態查找表DT  
void DestroyDSTable(BSTree *DT)  
{ 
  if(*DT) // 非空樹  
  { 
    if((*DT)->lchild) // 有左孩子  
      DestroyDSTable(&(*DT)->lchild); // 銷毀左孩子子樹  
    if((*DT)->rchild) // 有右孩子  
      DestroyDSTable(&(*DT)->rchild); // 銷毀右孩子子樹  
    free(*DT); // 釋放根結點  
    *DT=NULL; // 空指針賦0  
  } 
} 
 
// 在根指針T所指二叉排序樹中遞歸地查找某關鍵字等于key的數據元素，  
// 若查找成功，則返回指向該數據元素結點的指針,否則返回空指針。 
BSTree SearchBST(BSTree T,KeyType key) 
{ 
  if((!T)|| (key == T->data.key)) 
    return T; // 查找結束  
  else if(key < T->data.key) // 在左子樹中繼續查找  
    return SearchBST(T->lchild,key); 
  else 
    return SearchBST(T->rchild,key); // 在右子樹中繼續查找  
} 
 
// 對以*p為根的二叉排序樹作右旋處理，處理之后p指向新的樹根結點，即旋轉  
// 處理之前的左子樹的根結點。 
void R_Rotate(BSTree *p) 
{ 
  BSTree lc; 
  lc=(*p)->lchild; // lc指向p的左子樹根結點  
  (*p)->lchild=lc->rchild; // lc的右子樹掛接為p的左子樹  
  lc->rchild=*p; 
  *p=lc; // p指向新的根結點  
} 
 
// 對以*p為根的二叉排序樹作左旋處理，處理之后p指向新的樹根結點，即旋轉  
// 處理之前的右子樹的根結點。 
void L_Rotate(BSTree *p) 
{ 
  BSTree rc; 
  rc=(*p)->rchild; // rc指向p的右子樹根結點  
  (*p)->rchild=rc->lchild; // rc的左子樹掛接為p的右子樹  
  rc->lchild=*p; 
  *p=rc; // p指向新的根結點  
} 
 
// 對以指針T所指結點為根的二叉樹作左平衡旋轉處理，本算法結束時，  
// 指針T指向新的根結點。 
void LeftBalance(BSTree *T) 
{   
  BSTree lc,rd; 
  lc=(*T)->lchild; // lc指向*T的左子樹根結點  
  switch(lc->bf) 
  { // 檢查*T的左子樹的平衡度，并作相應平衡處理  
  case LH: // 新結點插入在*T的左孩子的左子樹上，要作單右旋處理  
    (*T)->bf=lc->bf=EH; 
    R_Rotate(T); 
    break; 
  case RH: // 新結點插入在*T的左孩子的右子樹上，要作雙旋處理  
    rd=lc->rchild; // rd指向*T的左孩子的右子樹根  
    switch(rd->bf) 
    { // 修改*T及其左孩子的平衡因子  
    case LH: 
      (*T)->bf=RH; 
      lc->bf=EH; 
      break; 
    case EH:  
      (*T)->bf=lc->bf=EH; 
      break; 
    case RH: 
      (*T)->bf=EH; 
      lc->bf=LH; 
    } 
    rd->bf=EH; 
    L_Rotate(&(*T)->lchild); // 對*T的左子樹作左旋平衡處理  
    R_Rotate(T); // 對*T作右旋平衡處理  
  } 
} 
 
// 對以指針T所指結點為根的二叉樹作右平衡旋轉處理，本算法結束時，  
// 指針T指向新的根結點 
void RightBalance(BSTree *T) 
{ 
  BSTree rc,rd; 
  rc=(*T)->rchild; // rc指向*T的右子樹根結點  
  switch(rc->bf) 
  { // 檢查*T的右子樹的平衡度，并作相應平衡處理  
  case RH: // 新結點插入在*T的右孩子的右子樹上，要作單左旋處理  
    (*T)->bf=rc->bf=EH; 
    L_Rotate(T); 
    break; 
  case LH: // 新結點插入在*T的右孩子的左子樹上，要作雙旋處理  
    rd=rc->lchild; // rd指向*T的右孩子的左子樹根  
    switch(rd->bf) 
    { // 修改*T及其右孩子的平衡因子  
    case RH: (*T)->bf=LH; 
      rc->bf=EH; 
      break; 
    case EH: (*T)->bf=rc->bf=EH; 
      break; 
    case LH: (*T)->bf=EH; 
      rc->bf=RH; 
    } 
    rd->bf=EH; 
    R_Rotate(&(*T)->rchild); // 對*T的右子樹作右旋平衡處理  
    L_Rotate(T); // 對*T作左旋平衡處理  
  } 
} 
 
// 若在平衡的二叉排序樹T中不存在和e有相同關鍵字的結點，則插入一個  
// 數據元素為e的新結點，并返回1，否則返回0。若因插入而使二叉排序樹  
// 失去平衡，則作平衡旋轉處理，布爾變量taller反映T長高與否。  
int InsertAVL(BSTree *T,ElemType e,int *taller) 
{ 
  if(!*T) 
  { // 插入新結點，樹“長高”，置taller為1  
    *T=(BSTree)malloc(sizeof(BSTNode)); 
    (*T)->data=e; 
    (*T)->lchild=(*T)->rchild=NULL; 
    (*T)->bf=EH; 
    *taller=1; 
  } 
  else 
  { 
    if(e.key == (*T)->data.key) 
    { // 樹中已存在和e有相同關鍵字的結點則不再插入  
      *taller=0; 
      return 0; 
    } 
    if(e.key < (*T)->data.key) 
    { // 應繼續在*T的左子樹中進行搜索  
      if(!InsertAVL(&(*T)->lchild,e,taller)) // 未插入  
        return 0; 
      if(*taller) 
        // 已插入到*T的左子樹中且左子樹“長高”  
        switch((*T)->bf) // 檢查*T的平衡度  
        { 
        case LH: 
          // 原本左子樹比右子樹高，需要作左平衡處理  
          LeftBalance(T); 
          *taller=0; //標志沒長高 
          break; 
        case EH: 
          // 原本左、右子樹等高，現因左子樹增高而使樹增高  
          (*T)->bf=LH; 
          *taller=1; //標志長高 
          break; 
        case RH: 
          // 原本右子樹比左子樹高，現左、右子樹等高 
          (*T)->bf=EH;  
          *taller=0; //標志沒長高 
      } 
    } 
    else 
    { 
      // 應繼續在*T的右子樹中進行搜索  
      if(!InsertAVL(&(*T)->rchild,e,taller)) // 未插入  
        return 0; 
      if(*taller) // 已插入到T的右子樹且右子樹“長高”  
        switch((*T)->bf) // 檢查T的平衡度  
      { 
      case LH:  
        (*T)->bf=EH; // 原本左子樹比右子樹高，現左、右子樹等高  
        *taller=0; 
        break; 
      case EH: // 原本左、右子樹等高，現因右子樹增高而使樹增高  
        (*T)->bf=RH; 
        *taller=1; 
        break; 
      case RH: // 原本右子樹比左子樹高，需要作右平衡處理  
        RightBalance(T); 
        *taller=0; 
      } 
    } 
  } 
  return 1; 
} 
 
// 按關鍵字的順序對DT的每個結點調用函數Visit()一次 
void TraverseDSTable(BSTree DT,void(*Visit)(ElemType)) 
{  
  if(DT) 
  { 
    TraverseDSTable(DT->lchild,Visit); // 先中序遍歷左子樹  
    Visit(DT->data); // 再訪問根結點  
    TraverseDSTable(DT->rchild,Visit); // 最后中序遍歷右子樹  
  } 
} 
 
 
void print(ElemType c) 
{ 
  printf("(%d,%d)",c.key,c.order); 
} 
 
int main() 
{ 
  BSTree dt,p; 
  int k; 
  int i; 
  KeyType j; 
  ElemType r[N]={ 
    {13,1},{24,2},{37,3},{90,4},{53,5} 
  }; // (以教科書P234圖9.12為例)  
   
  InitDSTable(&dt);  // 初始化空樹  
  for(i=0;i<N;i++) 
    InsertAVL(&dt,r[i],&k); // 建平衡二叉樹  
  TraverseDSTable(dt,print); // 按關鍵字順序遍歷二叉樹  
  printf("\n請輸入待查找的關鍵字: "); 
  scanf("%d",&j); 
  p=SearchBST(dt,j); // 查找給定關鍵字的記錄  
  if(p) 
    print(p->data); 
  else 
    printf("表中不存在此值"); 
  printf("\n"); 
  DestroyDSTable(&dt); 
   
  system("pause"); 
  return 0; 
} 
/* 
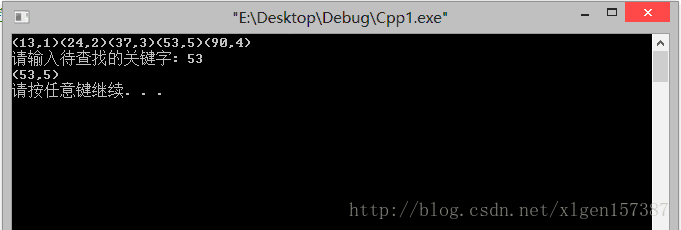
輸出效果： 
 
(13,1)(24,2)(37,3)(53,5)(90,4) 
請輸入待查找的關鍵字: 53 
(53,5) 
請按任意鍵繼續. . .  
 
*/

運行結果如下：

關于C語言中怎么實現一個平衡二叉樹就分享到這里了，希望以上內容可以對大家有一定的幫助，可以學到更多知識。如果覺得文章不錯，可以把它分享出去讓更多的人看到。