您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
并查集(Union-Find Set):
一種用于管理分組的數據結構。它具備兩個操作:(1)查詢元素a和元素b是否為同一組 (2) 將元素a和b合并為同一組。
注意:并查集不能將在同一組的元素拆分為兩組。
并查集的實現:
用樹來實現。
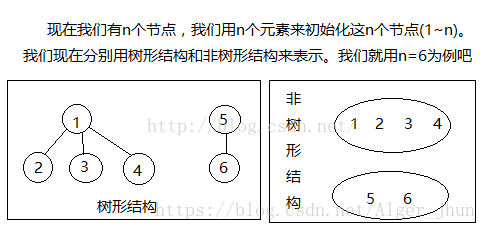
使用樹形結構來表示以后,每一組都對應一棵樹,然而我們就可以將這個問題轉化為樹的問題了,我們看兩個元素是否為一組我們只要看這兩個元素的根是否一致。顯然,使用樹形結構將問題簡單化了。合并時是我們只需要將一組的根與另一組的根相連即可。
并查集的核心在于,一棵樹的所有節點根節點都為一個節點。使用Find函數查詢時,也是查詢到這個節點的根節點。
一行并查集:
int find(int x)
{
return p[x]==x? x:find(p[x]); //x的父節點保存在p[x]中,如果沒有父節點則p[x]=x。
}
實現:
int node[i]; //每個節點
//初始化n個節點
void Init(int n){
for(int i = 0; i < n; i++){
node[i] = i;
}
}
//查找當前元素所在樹的根節點(代表元素)
int find(int x){
if(x == node[x])
return x;
return find(node[x]);
}
//合并元素x, y所處的集合
void Unite(int x, int y){
//查找到x,y的根節點
x = find(x);
y = find(y);
if(x == y)
return ;
//將x的根節點與y的根節點相連
node[x] = y;
}
//判斷x,y是屬于同一個集合
bool same(int x, int y){
return find(x) == find(y)
并查集的路徑壓縮:
在特殊情況下,這棵樹是一條長長的樹鏈,設鏈的最后一個結點為x,則每次執行find(x)都會遍歷整條鏈。效率十分的地下。 改進方法很簡單,只要把遍歷過的結點都改成根的子結點,后面的查詢就會變的快很多。
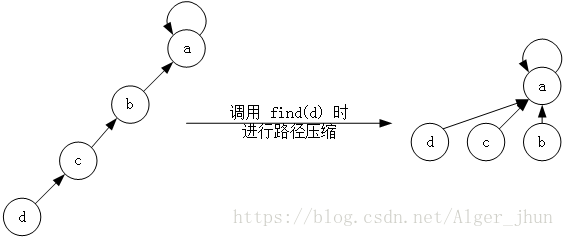
并查集的復雜度
加入這兩個優化之后,并查集的效率就非常高。對n個元素的并查集操作一次的復雜度是: O(α(n))。這里,α(n)是阿克曼(Ackermann)函數的反函數。效率要高于O(log n)。
不過這里O(α(n))是平均復雜度。也就是說,多次操作之后平均復雜度為O(α(n)),換而言之,并不是每一次操作都滿足O(α(n))。
路徑壓縮后的優化代碼:
int node[i]; //每個節點
int rank[i]; //樹的高度
//初始化n個節點
void Init(int n){
for(int i = 0; i < n; i++){
node[i] = i;
rank[i] = 0;
}
}
//查找當前元素所在樹的根節點(代表元素)
int find(int x){
if(x == node[x])
return x;
return node[x] = find(node[x]); //在第一次查找時,將節點直連到根節點
}
//合并元素x, y所處的集合
void Unite(int x, int y){
//查找到x,y的根節點
x = find(x);
y = find(y);
if(x == y)
return ;
//判斷兩棵樹的高度,然后在決定誰為子樹
if(rank[x] < rank[y]){
node[x] = y;
}else{
node[y] = x;
if(rank[x] == rank[y]) rank[x]++:
}
}
//判斷x,y是屬于同一個集合
bool same(int x, int y){
return find(x) == find(y);
}
實例分析:
題目:部落
在一個社區里,每個人都有自己的小圈子,還可能同時屬于很多不同的朋友圈。我們認為朋友的朋友都算在一個部落里,于是要請你統計一下,在一個給定社區中,到底有多少個互不相交的部落?并且檢查任意兩個人是否屬于同一個部落。
輸入格式:
輸入在第一行給出一個正整數N(<= 104),是已知小圈子的個數。隨后N行,每行按下列格式給出一個小圈子里的人:
K P[1] P[2] ... P[K]
其中K是小圈子里的人數,P[i](i=1, .., K)是小圈子里每個人的編號。這里所有人的編號從1開始連續編號,最大編號不會超過104。
之后一行給出一個非負整數Q(<= 104),是查詢次數。隨后Q行,每行給出一對被查詢的人的編號。
輸出格式:
首先在一行中輸出這個社區的總人數、以及互不相交的部落的個數。隨后對每一次查詢,如果他們屬于同一個部落,則在一行中輸出“Y”,否則輸出“N”。
輸入樣例:
4
3 10 1 2
2 3 4
4 1 5 7 8
3 9 6 4
2
10 5
3 7
輸出樣例:
10 2
Y
N
分析:典型并查集問題。
一個部落對應一個集合。 根節點數量等于部落數量。
并查集把每個部落的人連起來,記錄哪些人出現過,枚舉標號10000,找出有多少人和部落,查詢并查集維護。
源碼分析:
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int pre[10005];
int f[10005];
void init() { //初始化父集合pre[10005],以及出現的標志數組f[10005]
for(int i=0; i<10004; i++)
pre[i]=i, f[i]=0;
}
int find(int x) { //并查集查找根節點的 遞歸程序
return pre[x]==x? x : pre[x]=find(pre[x]);
}
int main()
{
init();
int n,q,k,a,b;
cin>>n;
for(int i=0; i<n; i++) {
cin>>k>>a;
f[a]=1;
for(int j=1; j<k; j++) {
cin>>b;
f[b]=1;
int x=find(a);
int y=find(b);
if(x!=y) pre[x]=y;
}
}
int cnt=0,tot=0; //cnt為所有人數 tot為部落數量
for(int i=0; i<10004; i++) {
if(f[i] == 1) { //如果標志為1 則說明出現過,cnt加一
cnt++;
if(pre[i]==i) tot++; //如果下標為本身 說明其為根節點 根節點數量為部落的數量
}
}
cout<<cnt<<" "<<tot<<endl;
cin>>q;
for(int i=0; i<q; i++) {
cin>>a>>b;
if(find(a) == find(b)) //若兩參數 有同一根節點 說明為一個部落。
cout<<"Y"<<endl;
else cout<<"N"<<endl;
}
return 0;
}
好了,這篇文章就介紹到這了。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。