您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
快速排序是一種基于分治技術的重要排序算法。不像歸并排序是按照元素在數組中的位置對它們進行劃分,快速排序按照元素的值對它們進行劃分。具體來說,它對給定數組中的元素進行重新排列,以得到一個快速排序的分區。在一個分區中,所有在s下標之前的元素都小于等于A[s],所有在s下標之后的元素都大于等于A[s]。
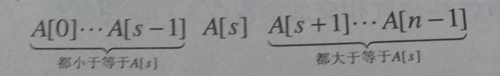
顯然,建立了一個分區以后,A[s]已經位于它在有序數組中的最終位置,接下來我們可以繼續對A[s]前和A[s]后的子數組分別進行排序(使用同樣的方法)。
為了排序一個數組A的全部元素,初始調用的是QUICKSORT(A,1,A.length)。
下面的算法對A[p..r]進行分區(先偽代碼一下、領會意思)。
PARTITION(A,p,r) x = A[r] i = p - 1 for j = p to r - 1 if A[j] ≤ x i = i + 1 exchange A[i] with A[j] exchange A[i+1] with A[r] return i+1
快速排序算法的效率:
在最優情況下,鍵值比較的次數Cbest(n)滿足下面的遞推式:
當n>1時,Cbest(n)=2Cbest(n/2)+n,Cbest(1)=0
根據主定理,Cbest(n)∈Θ(nlogn);對于n=2k的情況求得Cbest(n) = nlog(n)。
在最差的情況下,所有的分裂點都趨于極端:兩個子數組有一個為空,而另一個子數組僅僅比被分區的數組少一個元素。具體來說,這種令人遺憾的情況會發生在升序的數組上,也就是說輸入的數組已經被排過序了。所以,在進行了n+1次比較之后建立了分區,并且將A[0]和它本身進行了交換以后,快速排序算法還會對嚴格遞增的數組A[1..n-1]進行排序。對規模減小了的嚴格遞增數組的排序會一直繼續到最后一個子數組A[n-2..n-1]。這種情況下,鍵值比較的總次數應該等于:
Cworst(n)=(n+1)+n+...+3=(n+1)(n+2)/2-3∈Θ(n2)
現在,輪到討論快速排序在平均情況下的效率了。對于大小為n的隨機排列的數組,快速排序的平均鍵值比較次數記為Cavg(n)。假設分區的分裂點s(0≤s≤n-1)位于每個位置的概率都是1/n,我們得到下面的遞推關系式:
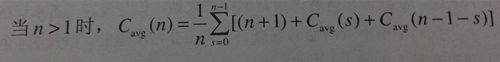
Cavg(0)=0,Cavg(1)=0
Cavg(n)≈2nlnn≈1.38nlogn
因此,快速排序在平均情況下,僅比最優情況多執行38%的比較操作。此外,它的最內層循環效率非常高,使得在處理隨機排列的數組時,速度要比歸并排序快。
以下是快速排序的Go代碼:
func QuickSort(slice_arg []int, iLeft int, iRight int) {
if iLeft < iRight {
var iTmpVal = slice_arg[iLeft]
var i, j = iLeft, iRight
for i < j {
fmt.Println("i,j = ", i, j)
for i < j && slice_arg[j] > iTmpVal {
j--
}
if i < j {
slice_arg[i] = slice_arg[j]
i++
}
for i < j && slice_arg[i] < iTmpVal {
i++
}
if i < j {
slice_arg[j] = slice_arg[i]
j--
}
}
slice_arg[i] = iTmpVal
QuickSort(slice_arg, iLeft, i-1)
QuickSort(slice_arg, j+1, iRight)
}
}
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。