使用javascript怎么實現一個trie前綴樹

本篇文章為大家展示了使用javascript怎么實現一個trie前綴樹，內容簡明扼要并且容易理解，絕對能使你眼前一亮，通過這篇文章的詳細介紹希望你能有所收獲。

Trie樹（來自單詞retrieval），又稱前綴字，單詞查找樹，字典樹，是一種樹形結構，是一種哈希樹的變種，是一種用于快速檢索的多叉樹結構。

它的優點是：最大限度地減少無謂的字符串比較，查詢效率比哈希表高。

Trie的核心思想是空間換時間。利用字符串的公共前綴來降低查詢時間的開銷以達到提高效率的目的。

Trie樹也有它的缺點, 假定我們只對字母與數字進行處理，那么每個節點至少有52＋10個子節點。為了節省內存，我們可以用鏈表或數組。在JS中我們直接用數組，因為JS的數組是動態的，自帶優化。

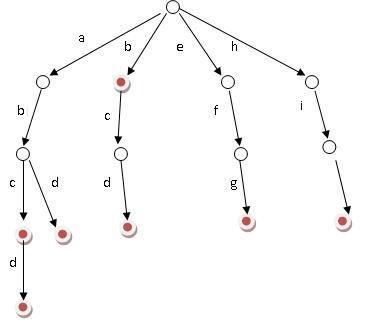
基本性質

1. 根節點不包含字符，除根節點外的每一個子節點都包含一個字符

2. 從根節點到某一節點。路徑上經過的字符連接起來，就是該節點對應的字符串

3. 每個節點的所有子節點包含的字符都不相同

程序實現

// by 司徒正美
class Trie {
 constructor() {
  this.root = new TrieNode();
 }
 isValid(str) {
  return /^[a-z1-9]+$/i.test(str);
 }
 insert(word) {
  // addWord
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //減少”0“的charCode
    var node = cur.son[c];
    if (node == null) {
     var node = (cur.son[c] = new TrieNode());
     node.value = word.charAt(i);
     node.numPass = 1; //有N個字符串經過它
    } else {
     node.numPass++;
    }
    cur = node;
   }
   cur.isEnd = true; //檣記有字符串到此節點已經結束
   cur.numEnd++; //這個字符串重復次數

   return true;
  } else {
   return false;
  }
 }
 remove(word){
   if (this.isValid(word)) {
     var cur = this.root;
     var array = [], n = word.length
     for (var i = 0; i < n; i++) {
       var c = word.charCodeAt(i);
       c = this.getIndex(c)
       var node = cur.son[c];
       if(node){
         array.push(node)
         cur = node
       }else{
         return false
       }
 
     }
     if(array.length === n){
       array.forEach(function(){
         el.numPass--
       })
       cur.numEnd --
       if( cur.numEnd == 0){
         cur.isEnd = false
       } 
     }
   }else{
     return false
   }
 }
 preTraversal(cb){//先序遍歷
    function preTraversalImpl(root, str, cb){ 
      cb(root, str);
      for(let i = 0,n = root.son.length; i < n; i ++){
        let node = root.son[i];
        if(node){
          preTraversalImpl(node, str + node.value, cb);
        }
      }
    } 
    preTraversalImpl(this.root, "", cb);
  }
 // 在字典樹中查找是否存在某字符串為前綴開頭的字符串(包括前綴字符串本身)
 isContainPrefix(word) {
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //減少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return false;
    }
   }
   return true;
  } else {
   return false;
  }
 }
 isContainWord(str) {
  // 在字典樹中查找是否存在某字符串(不為前綴)
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //減少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return false;
    }
   }
   return cur.isEnd;
  } else {
   return false;
  }
 }
 countPrefix(word) {
  // 統計以指定字符串為前綴的字符串數量
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //減少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return 0;
    }
   }
   return cur.numPass;
  } else {
   return 0;
  }
 }
 countWord(word) {
  // 統計某字符串出現的次數方法
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //減少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return 0;
    }
   }
   return cur.numEnd;
  } else {
   return 0;
  }
 }
}

class TrieNode {
 constructor() {
  this.numPass = 0;//有多少個單詞經過這節點
  this.numEnd = 0; //有多少個單詞就此結束
  this.son = [];
  this.value = ""; //value為單個字符
  this.isEnd = false;
 }
}

我們重點看一下TrieNode與Trie的insert方法。 由于字典樹是主要用在詞頻統計，因此它的節點屬性比較多, 包含了numPass, numEnd但非常重要的屬性。

insert方法是用于插入重詞，在開始之前，我們必須判定單詞是否合法，不能出現 特殊字符與空白。在插入時是打散了一個個字符放入每個節點中。每經過一個節點都要修改numPass。

優化

現在我們每個方法中，都有一個c=-48的操作，其實數字與大寫字母與小寫字母間其實還有其他字符的，這樣會造成無謂的空間的浪費

// by 司徒正美
getIndex(c){
   if(c < 58){//48-57
     return c - 48
   }else if(c < 91){//65-90
     return c - 65 + 11
   }else {//> 97 
     return c - 97 + 26+ 11
   }
 }

然后相關方法將c-= 48改成c = this.getIndex(c)即可

測試

var trie = new Trie(); 
  trie.insert("I"); 
  trie.insert("Love"); 
  trie.insert("China"); 
  trie.insert("China"); 
  trie.insert("China"); 
  trie.insert("China"); 
  trie.insert("China"); 
  trie.insert("xiaoliang"); 
  trie.insert("xiaoliang"); 
  trie.insert("man"); 
  trie.insert("handsome"); 
  trie.insert("love"); 
  trie.insert("Chinaha"); 
  trie.insert("her"); 
  trie.insert("know"); 
  var map = {}
  trie.preTraversal(function(node, str){
    if(node.isEnd){
     map[str] = node.numEnd
    }
  })
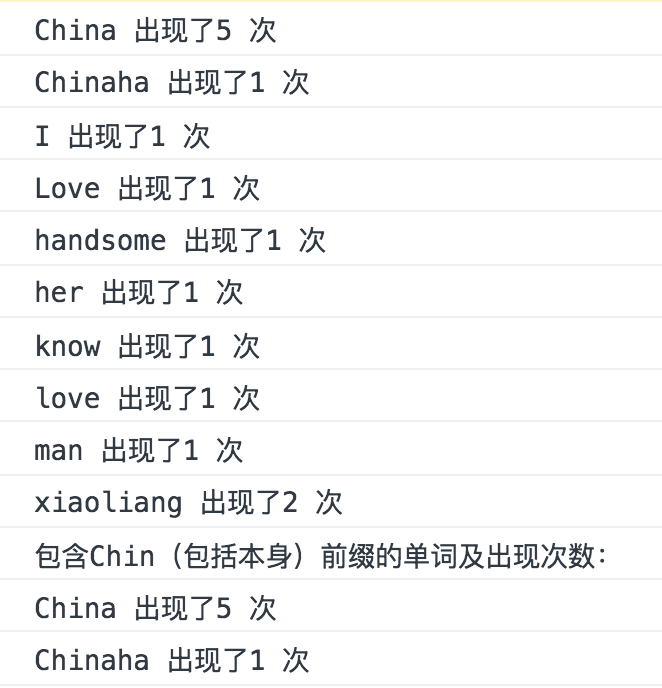
  for(var i in map){
    console.log(i+" 出現了"+ map[i]+" 次")
  }
  console.log("包含Chin（包括本身）前綴的單詞及出現次數："); 
  //console.log("China")
  var map = {}
  trie.preTraversal(function(node, str){
    if(str.indexOf("Chin") === 0 && node.isEnd){
      map[str] = node.numEnd
    }
   })
  for(var i in map){
    console.log(i+" 出現了"+ map[i]+" 次")
  }

Trie樹和其它數據結構的比較

Trie樹與二叉搜索樹

二叉搜索樹應該是我們最早接觸的樹結構了，我們知道，數據規模為n時，二叉搜索樹插入、查找、刪除操作的時間復雜度通常只有O(log n)，最壞情況下整棵樹所有的節點都只有一個子節點，退變成一個線性表，此時插入、查找、刪除操作的時間復雜度是O(n)。

通常情況下，Trie樹的高度n要遠大于搜索字符串的長度m，故查找操作的時間復雜度通常為O(m)，最壞情況下的時間復雜度才為O(n)。很容易看出，Trie樹最壞情況下的查找也快過二叉搜索樹。

文中Trie樹都是拿字符串舉例的，其實它本身對key的適宜性是有嚴格要求的，如果key是浮點數的話，就可能導致整個Trie樹巨長無比，節點可讀性也非常差，這種情況下是不適宜用Trie樹來保存數據的；而二叉搜索樹就不存在這個問題。

Trie樹與Hash表

考慮一下Hash沖突的問題。Hash表通常我們說它的復雜度是O(1)，其實嚴格說起來這是接近完美的Hash表的復雜度，另外還需要考慮到hash函數本身需要遍歷搜索字符串，復雜度是O(m)。在不同鍵被映射到“同一個位置”（考慮closed hashing，這“同一個位置”可以由一個普通鏈表來取代）的時候，需要進行查找的復雜度取決于這“同一個位置”下節點的數目，因此，在最壞情況下，Hash表也是可以成為一張單向鏈表的。

Trie樹可以比較方便地按照key的字母序來排序（整棵樹先序遍歷一次就好了），這跟絕大多數Hash表是不同的（Hash表一般對于不同的key來說是無序的）。

在較理想的情況下，Hash表可以以O(1)的速度迅速命中目標，如果這張表非常大，需要放到磁盤上的話，Hash表的查找訪問在理想情況下只需要一次即可；但是Trie樹訪問磁盤的數目需要等于節點深度。

很多時候Trie樹比Hash表需要更多的空間，我們考慮這種一個節點存放一個字符的情況的話，在保存一個字符串的時候，沒有辦法把它保存成一個單獨的塊。Trie樹的節點壓縮可以明顯緩解這個問題，后面會講到。

Trie樹的改進

按位Trie樹（Bitwise Trie）

原理上和普通Trie樹差不多，只不過普通Trie樹存儲的最小單位是字符，但是Bitwise Trie存放的是位而已。位數據的存取由CPU指令一次直接實現，對于二進制數據，它理論上要比普通Trie樹快。

節點壓縮。

分支壓縮：對于穩定的Trie樹，基本上都是查找和讀取操作，完全可以把一些分支進行壓縮。例如，前圖中最右側分支的inn可以直接壓縮成一個節點“inn”，而不需要作為一棵常規的子樹存在。Radix樹就是根據這個原理來解決Trie樹過深問題的。

節點映射表：這種方式也是在Trie樹的節點可能已經幾乎完全確定的情況下采用的，針對Trie樹中節點的每一個狀態，如果狀態總數重復很多的話，通過一個元素為數字的多維數組（比如Triple Array Trie）來表示，這樣存儲Trie樹本身的空間開銷會小一些，雖說引入了一張額外的映射表。

前綴樹的應用

前綴樹還是很好理解，它的應用也是非常廣的。

（1）字符串的快速檢索

字典樹的查詢時間復雜度是O(logL)，L是字符串的長度。所以效率還是比較高的。字典樹的效率比hash表高。

（2）字符串排序

從上圖我們很容易看出單詞是排序的，先遍歷字母序在前面。減少了沒必要的公共子串。

（3）最長公共前綴

inn和int的最長公共前綴是in，遍歷字典樹到字母n時，此時這些單詞的公共前綴是in。

（4）自動匹配前綴顯示后綴

上述內容就是使用javascript怎么實現一個trie前綴樹，你們學到知識或技能了嗎？如果還想學到更多技能或者豐富自己的知識儲備，歡迎關注億速云行業資訊頻道。