您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本文為大家分享了Python機器學習之K-Means聚類的實現代碼,供大家參考,具體內容如下
1.K-Means聚類原理
K-means算法是很典型的基于距離的聚類算法,采用距離作為相似性的評價指標,即認為兩個對象的距離越近,其相似度就越大。其基本思想是:以空間中k個點為中心進行聚類,對最靠近他們的對象歸類。通過迭代的方法,逐次更新各聚類中心的值,直至得到最好的聚類結果。各聚類本身盡可能的緊湊,而各聚類之間盡可能的分開。
算法大致流程為:(1)隨機選取k個點作為種子點(這k個點不一定屬于數據集);(2)分別計算每個數據點到k個種子點的距離,離哪個種子點最近,就屬于哪類;(3)重新計算k個種子點的坐標(簡單常用的方法是求坐標值的平均值作為新的坐標值;(4)重復2、3步,直到種子點坐標不變或者循環次數完成。
2.數據及其尋找初步的聚類中心
數據為Matlab加載格式(mat),包含X變量,數據來源為(大家可以去這下載),X為300*2維變量,由于是2維,所以基本上就是在平面坐標軸上的一些點中進行聚類。
我們首先構建初步尋找聚類中心(centroids,質心)函數,再隨機設置初始質心,通過歐氏距離初步判斷X的每一個變量屬于哪個質心。代碼為:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
def find_closest_centroids(X, centroids):
m = X.shape[0]
k = centroids.shape[0] #要聚類的類別個數
idx = np.zeros(m)
for i in range(m):
min_dist = 1000000 #迭代終止條件
for j in range(k):
dist = np.sum((X[i,:] - centroids[j,:]) ** 2)
if dist < min_dist:
# 記錄當前最短距離和其中心的索引值
min_dist = dist
idx[i] = j
return idx
data = loadmat('D:\python\Python ml\ex7data2.mat')
X = data['X']
initial_centroids = np.array([[3, 3], [6, 2], [8, 5]])
idx = find_closest_centroids(X, initial_centroids)
idx[0:3]
在這里先生成m(這里為300)個0向量,即idx,也就是假設X的每個變量均屬于0類,然后再根據與初始質心的距離計算dist = np.sum((X[i,:] - centroids[j,:]) ** 2),初步判斷每個變量歸屬哪個類,最終替代idx中的0.
3.不斷迭代尋找質心的位置并實現kmeans算法
上述idx得到的300維向量是判斷X中每個變量的歸屬類別,在此基礎上,再對初始質心集群位置不斷調整,尋找最優質心。
def compute_centroids(X, idx, k):
m, n = X.shape
centroids = np.zeros((k, n))
for i in range(k):
indices = np.where(idx == i)
centroids[i,:] = (np.sum(X[indices,:], axis=1) / len(indices[0])).ravel()
#這里簡單的將該類中心的所有數值求平均值作為新的類中心
return centroids
compute_centroids(X, idx, 3)
根據上述函數,來構建kmeans函數實現K-means聚類算法。然后根據得到的每個變量歸屬類別與質心坐標,進行可視化。
def run_k_means(X, initial_centroids, max_iters):
m, n = X.shape
k = initial_centroids.shape[0]
idx = np.zeros(m)
centroids = initial_centroids
for i in range(max_iters):
idx = find_closest_centroids(X, centroids)
centroids = compute_centroids(X, idx, k)
return idx, centroids
idx, centroids = run_k_means(X, initial_centroids, 10)
cluster1 = X[np.where(idx == 0)[0],:] #獲取X中屬于第一個類別的數據集合,即類別1的點
cluster2 = X[np.where(idx == 1)[0],:]
cluster3 = X[np.where(idx == 2)[0],:]
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(cluster1[:,0], cluster1[:,1], s=30, color='r', label='Cluster 1')
ax.scatter(cluster2[:,0], cluster2[:,1], s=30, color='g', label='Cluster 2')
ax.scatter(cluster3[:,0], cluster3[:,1], s=30, color='b', label='Cluster 3')
ax.legend()
plt.show()
得到圖形如下:
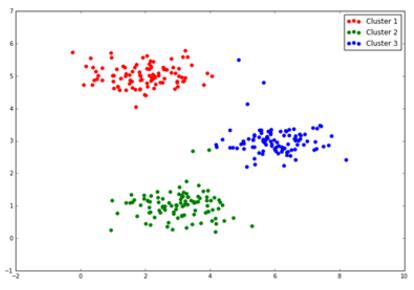
image.png
4.關于初始化質心的設置
我們前邊設置的初始質心:[3, 3], [6, 2], [8, 5],是事先設定的,并由此生成idx(每一變量歸屬類別的向量),這是后邊進行kmeans聚類的基礎,實際上對于二維以上數據,由于無法在平面坐標軸展示,很難一開始就設定較好的初始質心,另外,初始質心的設定也可能會影響算法的收斂性。所以需要我們再構造個初始化質心設定函數,來更好地設置初始質心。
def init_centroids(X, k):
m, n = X.shape
centroids = np.zeros((k, n)) #初始化零矩陣
idx = np.random.randint(0, m, k) #返回0-m之間的整數值
for i in range(k):
centroids[i,:] = X[idx[i],:]
return centroids
init_centroids(X, 3)
這里所生成的初始質心位置,其實就是從X的數據中隨機找3個變量作為初始值。在此基礎上,令initial_centroids = init_centroids(X, 3),然后代入前邊的code中,重新運行一遍即可。
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。