您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
多元函數擬合。如 電視機和收音機價格多銷售額的影響,此時自變量有兩個。
python 解法:
import numpy as np
import pandas as pd
#import statsmodels.api as sm #方法一
import statsmodels.formula.api as smf #方法二
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
df = pd.read_csv('http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv', index_col=0)
X = df[['TV', 'radio']]
y = df['sales']
#est = sm.OLS(y, sm.add_constant(X)).fit() #方法一
est = smf.ols(formula='sales ~ TV + radio', data=df).fit() #方法二
y_pred = est.predict(X)
df['sales_pred'] = y_pred
print(df)
print(est.summary()) #回歸結果
print(est.params) #系數
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d') #ax = Axes3D(fig)
ax.scatter(X['TV'], X['radio'], y, c='b', marker='o')
ax.scatter(X['TV'], X['radio'], y_pred, c='r', marker='+')
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()
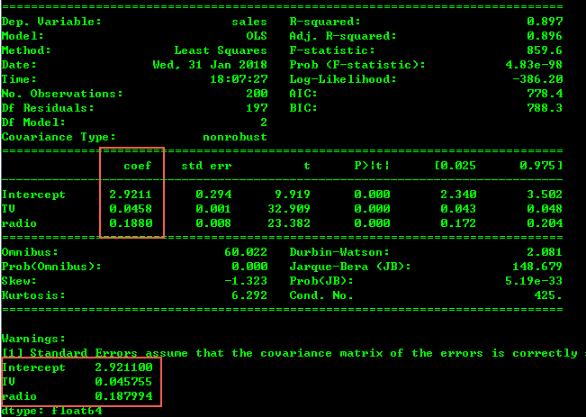
擬合的各項評估結果和參數都打印出來了,其中結果函數為:
f(sales) = β0 + β1*[TV] + β2*[radio]
f(sales) = 2.9211 + 0.0458 * [TV] + 0.188 * [radio]
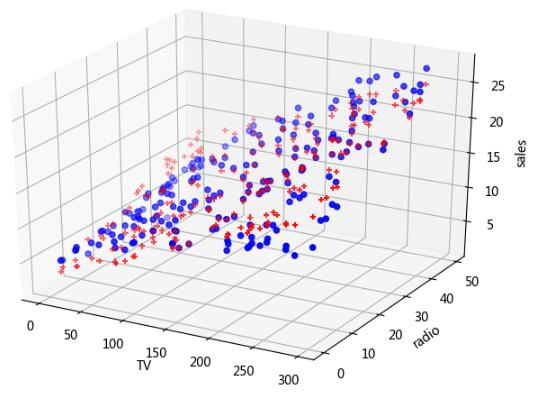
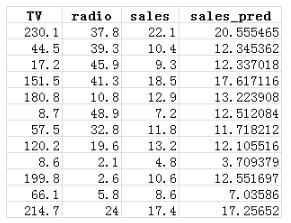
圖中,sales 方向上,藍色點為原 sales 實際值,紅色點為擬合函數計算出來的值。其實誤差并不大,部分數據如下。
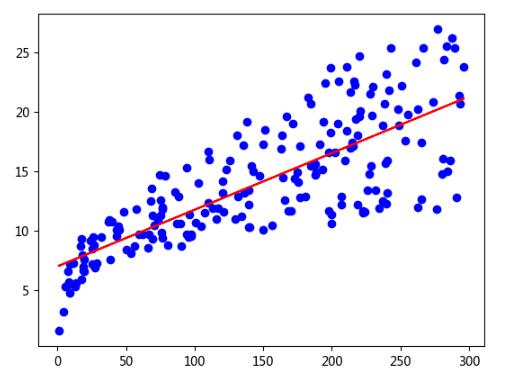
同樣可擬合一元函數;
import numpy as np
import pandas as pd
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
df = pd.read_csv('http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv', index_col=0)
X = df['TV']
y = df['sales']
est = smf.ols(formula='sales ~ TV ', data=df).fit()
y_pred = est.predict(X)
print(est.summary())
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(X, y, c='b')
ax.plot(X, y_pred, c='r')
plt.show()

Ridge Regression:(嶺回歸交叉驗證)
嶺回歸(ridge regression, Tikhonov regularization)是一種專用于共線性數據分析的有偏估計回歸方法,實質上是一種改良的最小二乘估計法,通過放棄最小二乘法的無偏性,以損失部分信息、降低精度為代價獲得回歸系數更為符合實際、更可靠的回歸方法,對病態數據的擬合要強于最小二乘法。通常嶺回歸方程的R平方值會稍低于普通回歸分析,但回歸系數的顯著性往往明顯高于普通回歸,在存在共線性問題和病態數據偏多的研究中有較大的實用價值。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model
from mpl_toolkits.mplot3d import Axes3D
df = pd.read_csv('http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv', index_col=0)
X = np.asarray(df[['TV', 'radio']])
y = np.asarray(df['sales'])
clf = linear_model.RidgeCV(alphas=[i+1 for i in np.arange(200.0)]).fit(X, y)
y_pred = clf.predict(X)
df['sales_pred'] = y_pred
print(df)
print("alpha=%s, 常數=%.2f, 系數=%s" % (clf.alpha_ ,clf.intercept_,clf.coef_))
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(df['TV'], df['radio'], y, c='b', marker='o')
ax.scatter(df['TV'], df['radio'], y_pred, c='r', marker='+')
ax.set_xlabel('TV')
ax.set_ylabel('radio')
ax.set_zlabel('sales')
plt.show()
輸出結果:alpha=150.0, 常數=2.94, 系數=[ 0.04575621 0.18735312]
以上這篇Python 普通最小二乘法(OLS)進行多項式擬合的方法就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。