您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要為大家展示了“Python如何實現遞歸算法”,內容簡而易懂,條理清晰,希望能夠幫助大家解決疑惑,下面讓小編帶領大家一起研究并學習一下“Python如何實現遞歸算法”這篇文章吧。
1. 遞歸概述
遞歸( recursion)是一種編程技巧,某些情況下,甚至是無可替代的技巧。遞歸可以大幅簡化代碼,看起來非常簡潔,但遞歸設計卻非常抽象,不容易掌握。通常,我們都是自上而下的思考問題, 遞歸則是自下而上的解決問題——這就是遞歸看起來不夠直觀的原因。那么,究竟什么是遞歸呢?讓我們先從生活中找一個栗子。
我們都有在黑暗的放映廳里找座位的經驗:問問前排的朋友坐的是第幾排,加上一,就是自己當前所處位置的排號。如果前排的朋友不知道自己是第幾排,他可以用同樣的方法得到自己的排號,然后再告訴你。如果前排的前排的朋友也不知道自己是第幾排,他就如法炮制。這樣的推導,不會無限制地進行下去,因為問到第一排的時候,坐在第一排的朋友一定會直接給出答案的。這就是遞歸算法在生活中的應用實例。
關于遞歸,不太嚴謹的定義是“一個函數在運行時直接或間接地調用了自身”。嚴謹一點的話,一個遞歸函數必須滿足下面兩個條件:
至少有一個明確的遞歸結束條件,我們稱之為遞歸出口,也有人喜歡把該條件叫做遞歸基。
有向遞歸出口方向靠近的直接或間接的自身調用(也被稱作遞歸調用)。
遞歸雖然晦澀,亦有規律可循。掌握了基本的遞歸理論,才有可能將其應用于復雜的算法設計中。
2. 線性遞歸
我們先從最經典的兩個遞歸算法開始——階乘(factorial)和斐波那契數列(Fibonacci sequence)。幾乎所有討論遞歸算法的話題,都是從從它們開始的。階乘的概念比較簡單,唯一需要說明的是,0的階乘是1而非0。為此,我專門請教了我的女兒,她是數學專業的學生。斐波那契數列,又稱黃金分割數列,指的是這樣一個數列:1、1、2、3、5、8、13、21、34、……在數學上,斐波納契數列是這樣定義的:
F(0)=1,F(1)=1, F(n)=F(n-1)+F(n-2)(n>=2,n∈N,N為正整數集)
階乘和斐波那契數列的遞歸算法如下:
def factorial(n): if n == 0: # 遞歸出口 return 1 return n*factorial(n-1) # 向遞歸出口方向靠近的自身調用 def fibonacci(n): if n < 2: # 遞歸出口 return 1 return fibonacci(n-1) + fibonacci(n-2) # 向遞歸出口方向靠近的自身調用
這兩個函數的結構都非常簡單,遞歸出口和自身調用清晰明了,但二者有一個顯著的區別:階乘函數中,只用一次自身調用,而斐波那契函數則有兩次自身調用。
階乘遞歸函數每一層的遞歸對自身的調用只有一次,因此每一層次上至多只有一個實例,且它們構成一個線性的次序關系。此類遞歸模式稱作“線性遞歸”,這是遞歸最基本形式。非線性遞歸(比如斐波那契遞歸函數)在每一層上都會產生兩個實例,時間復雜度為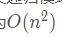 ,極易導致堆棧溢出。
,極易導致堆棧溢出。
其實,用循環的方法同樣可以簡潔地寫出上面兩個函數。的確,很多情況下,遞歸能夠解決的問題,循環也可以做到。但是,更多的情況下,循環是無法取代遞歸的。因此,深入研究遞歸理論是非常有必要的。
3. 尾遞歸
接下來,我們將上面的階乘遞歸函數改造一下,仍然用遞歸的方式實現。為了便于比較,我們把兩種算法放在一起。
def factorial_A(n): if n == 0: # 遞歸出口 return 1 return n*factorial_A(n-1) # 向遞歸出口方向靠近的自身調用 def factorial_B(n, k=1): if n == 0: # 遞歸出口 return k k *= n n -= 1 return factorial_B(n,k) # 向遞歸出口方向靠近的自身調用
比較 factorial_A() 和 factorial_B() 的寫法,就會發現很有意思的問題。factorial_A() 的自身調用屬于表達式的一部分,這意味著自身調用不是函數的最后一步,而是拿到自身調用的結果后,需要再做一次乘法運算;factorial_B() 的自身調用則是函數的最后一步。像 factorial_B() 函數這樣,當自身調用是整個函數體中最后執行的語句,且它的返回值不屬于表達式的一部分時,這個遞歸調用就是尾遞歸(Tail Recursion)。尾遞歸函數的特點是在回歸過程中不用做任何操作,這個特性很重要,因為大多數現代的編譯器會利用這種特點自動生成優化的代碼。
分別使用 factorial_A() 和 factorial_B() 計算5的階乘,下圖所示的計算過程,清晰展示了尾遞歸的優勢:不用花費大量的棧空間來保存上次遞歸中的參數、局部變量等,這是因為上次遞歸操作結束后,已經將之前的數據計算出來,傳遞給當前的遞歸函數,這樣上次遞歸中的局部變量和參數等就會被刪除,釋放空間,從而不會造成棧溢出。
factorial_A(5) 5 * factorial_A(4) 5 * 4 * factorial_A(3) 5 * 4 * 3 * factorial_A(2) 5 * 4 * 3 * 2 * factorial_A(1) 5 * 4 * 3 * 2 * 1 * factorial_A(0) 5 * 4 * 3 * 2 * 1 5 * 4 * 3 * 2 5 * 4 * 6 5 * 24 120 factorial_B(5, k=1) factorial_B(4, k=5) factorial_B(3, k=20) factorial_B(2, k=60) factorial_B(1, k=120) factorial_B(0, k=120) 120
尾遞歸雖然有低耗高效的優勢,但這一類遞歸一般都可轉化為循環語句。
4. 單向遞歸
前文中兩個遞歸函數,不管是階乘還是斐波那契數列,遞歸總是向著遞歸出口方向進行,沒有分支,沒有反復,這樣的遞歸,我們稱之為單向遞歸。在文件遞歸遍歷等應用場合,搜索完一個文件夾,通常要返回至父級目錄,繼續搜索其他兄弟文件夾,這個過程就不是單向的,而是有分叉的、帶回溯的。通常復雜遞歸都不是單向的,算法設計起來就比較困難。
import os def ergodic(folder): for root, dirs, files in os.walk(folder): for dir_name in dirs: print(os.path.join(root, dir_name)) for file_name in files: print(os.path.join(root, file_name))
上面是借助于 os 模塊的 walk() 實現的基于循環的文件遍歷方法。雖然是循環結構,如果不熟悉 walk() 的話,這個函數看起來還是很不直觀。我更喜歡下面的遞歸遍歷方法。
import os def ergodic(folder): for item in os.listdir(folder): obj = os.path.join(folder, item) print(obj) if os.path.isdir(obj): ergodic(obj)
5. 深度優先與廣度優先
遍歷文件通常有兩種策略:深度優先搜索 DFS(depth-first search) 和廣度優先搜索BFS(breadth-first search) 。顧名思義,深度優先就是優先處理本級文件夾中的子文件夾,遞歸向縱深發展;廣度優先就是優先處理本級文件夾中的文件,遞歸向水平方向發展。
import os def ergodic_DFS(folder): """基于深度優先的文件遍歷""" dirs, files = list(), list() for item in os.listdir(folder): if os.path.isdir(os.path.join(folder, item)): dirs.append(item) else: files.append(item) for dir_name in dirs: ergodic(os.path.join(folder, dir_name)) for file_name in files print(os.path.join(folder, file_name)) def ergodic_BFS(folder): """基于廣度優先的文件遍歷""" dirs, files = list(), list() for item in os.listdir(folder): if os.path.isdir(os.path.join(folder, item)): dirs.append(item) else: files.append(item) for file_name in files print(os.path.join(folder, file_name)) for dir_name in dirs: ergodic(os.path.join(folder, dir_name))
以上是“Python如何實現遞歸算法”這篇文章的所有內容,感謝各位的閱讀!相信大家都有了一定的了解,希望分享的內容對大家有所幫助,如果還想學習更多知識,歡迎關注億速云行業資訊頻道!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。