python中樹是什么

這篇文章給大家分享的是有關python中樹是什么的內容。小編覺得挺實用的，因此分享給大家做個參考，一起跟隨小編過來看看吧。

一、什么是樹

客觀世界中許多事物存在層次關系

人類社會家譜社會組織結構圖書信息管理

其中，人類社會家譜如下圖所示：

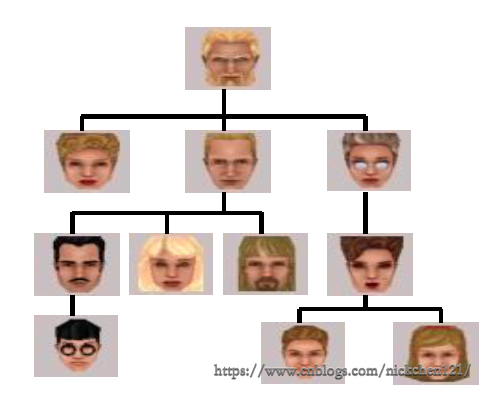
通過上述所說的分層次組織，能夠使我們在數據的管理上有更高的效率！那么，對于數據管理的基本操作——查找，我們如何實現有效率的查找呢？

二、查找

查找：根據某個給定關鍵字K，從集合R中找出關鍵字與K相同的記錄

靜態查找：集合中記錄是固定的，即對集合的操作沒有插入和刪除，只有查找

動態查找：集合中記錄是動態變化的，即對集合的操作既有查找，還可能發生插入和刪除（動態查找不在我們考慮范圍內）

2.1 靜態查找 2.1.1 方法1：順序查找

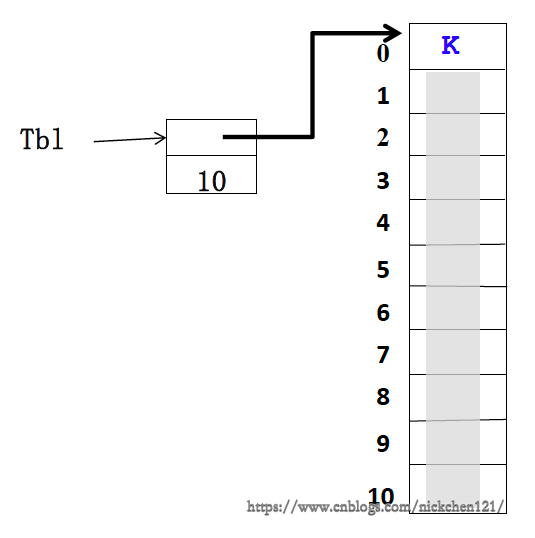
/* c語言實現 */

int SequentialSearch (StaticTable *Tbl, ElementType K)
{
// 在表Tbl[1]~Tb1[n]中查找關鍵字為K的數據元素
 int i;
 Tbl->Element[0] = K; // 建立哨兵，即沒找到可以返回哨兵的索引0表示未找到
 for (i = Tbl->Length; Tbl->Element[i] != K; i--); // 查找成功返回所在單元下標；不成功放回0
 return i;
}

順序查找算法的時間復雜度為O(n)

2.1.2 方法2：二分查找（Binary Search）

假設n個數據元素的關鍵字滿足有序（比如：小到大），即\(k_1<k_2<\cdots<k_n\)，并且是連續存放（數組），那么可以進行二分查找。

例：假設有13個數據元素，按關鍵字由小到大順序存放。二分查找關鍵字為444的數據元素過程如下圖：

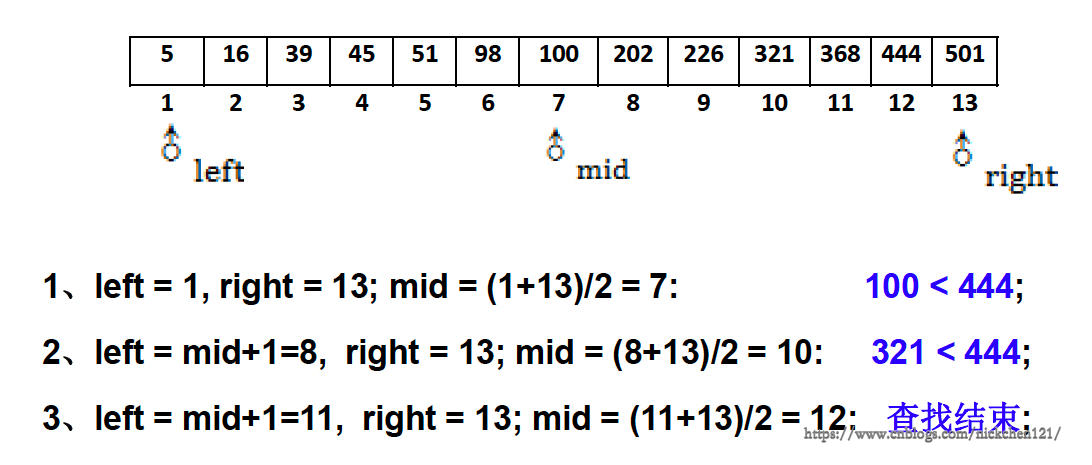
仍然以上面13個數據元素構成的有序線性表為例，二分查找關鍵字為43的數據元素如下圖：

/* c語言實現 */

int BinarySearch (StaticTable *Tbl, ElementType K)
{
 // 在表中Tbl中查找關鍵字為K的數據元素
 int left, right, mid, NoFound = -1;
 
 left = 1; // 初始左邊界
 right = Tbl->Length; // 初始右邊界
 while (left <= right)
 {
  mid = (left + right) / 2; // 計算中間元素坐標
  if (K < Tbl->Element[mid]) right = mid - 1; // 調整右邊界
  else if (K > Tbl->Element[mid]) left = mid + 1; // 調整左邊界
  else return mid; // 查找成功，返回數據元素的下標
 }
 return NotFound; // 查找不成功，返回-1
}

# python語言實現

def binary_chop(alist, data):
  n = len(alist)
  first = 0
  last = n - 1
  while first <= last:
    mid = (last + first) // 2
    if alist[mid] > data:
      last = mid - 1
    elif alist[mid] < data:
      first = mid + 1
    else:
      return True
  return False

二分查找算法具有對數的時間復雜度O(logN)

二分查找算法雖然解決了查找的時間復雜度問題，但是對于數據的插入和刪除確是O(n)的，因此有沒有一種數據結構，既可以減少數據查找的時間復雜度，又可以減少數據的插入和刪除的復雜度呢？

三、二分查找判定樹

除了使用上述兩個方法進行關鍵字的查找，我們還可以通過二叉樹這種數據結構完成關鍵字的查找。

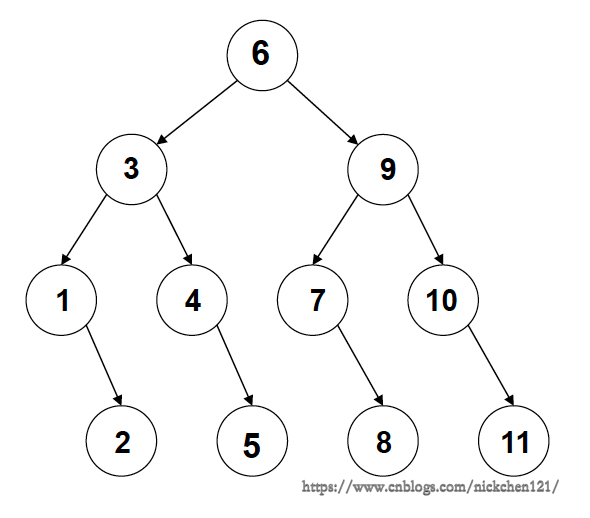
從上圖可以看出，如果我們需要尋找數字8，可以通過以下4步實現（可能看不懂，未來會看得懂）：

根節點6小于8，往6的右子節點9找結點9大于8，往9的左子結點7找結點7小于8，往7的左子結點找找到8 判定樹上每個結點需要的查找次數剛好為該結點所在的層數；查找成功時查找次數不會超過判定樹的深度 N個結點的判定樹的深度為\([log_2{n}]+1\) \(ASL = (4*4+4*3+2*2+1)/11 = 3\) 四、樹的定義

樹（Tree）：\(n(n\geq{0})\)個結點構成的有限集合。

當n=0時，稱為空樹對于任一顆非空樹（n>0），它具備以下性質： 樹中有一個稱為根（Root）的特殊結點，用r表示其余結點可分為m（m>0）個互不相交的有限集\(T_1,T_2,\cdots,T_m\)，其中每個集合本身又是一棵樹，稱為原來樹的子樹（SubTree）

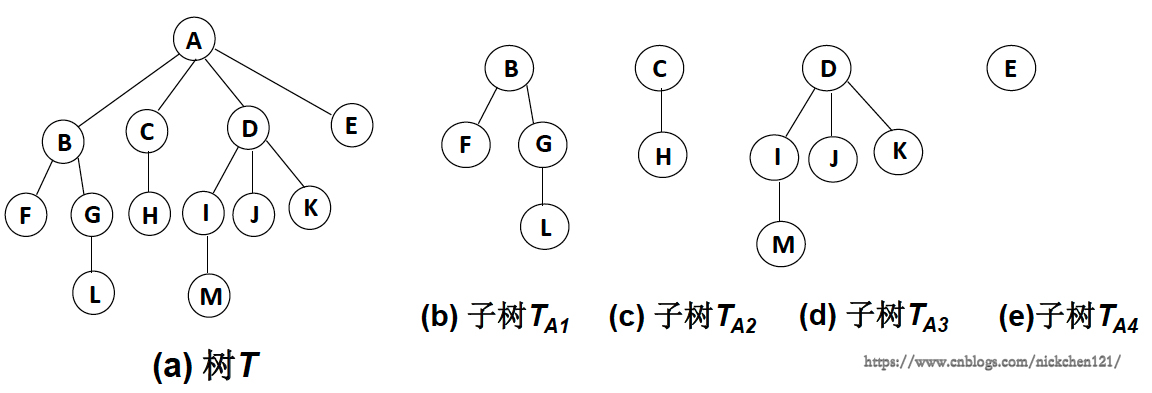
五、樹與非樹

牢記樹有以下3個特性：

子樹是不相交的；除了根結點外，每個結點有且僅有一個父結點；一顆N個結點的樹有N-1條邊 5.1 非樹

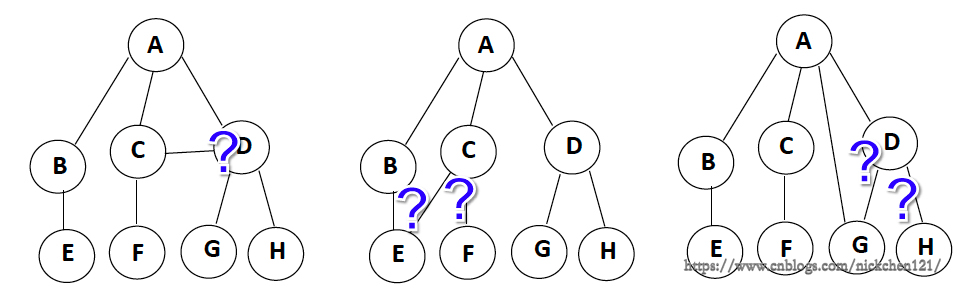
5.2 樹

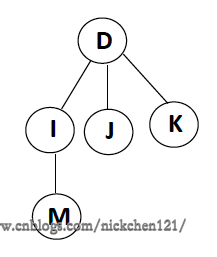
六、樹的一些基本術語

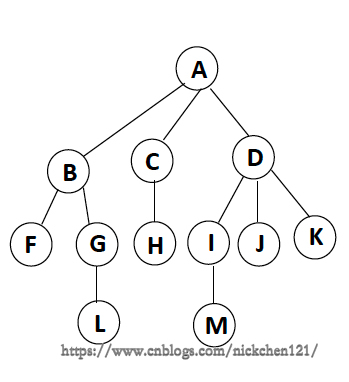
結點的度（Degree）：結點的子樹個數樹的度：樹的所有結點中最大的度數葉結點（Leaf）： 度為0的結點父結點（Parent）：有子樹的結點是其子樹的根結點的父結點子結點（Child）：若A結點是B結點的父結點，則稱B結點是A結點的子結點；子結點也稱孩子結點

兄弟結點（Sibling）：具有同一父結點的各結點彼此是兄弟結點

路徑和路徑長度：從結點\(n_1\)到\(n_k\)的路徑為一個結點序列\(n_1 , n_2 ,\cdots, n_k\) , \(n_i\)是\(n_{i+1}\)的父結點。路徑所包含邊的個數為路徑的長度

祖先結點(Ancestor)：沿樹根到某一結點路徑上的所有結點都是這個結點的祖先結點

子孫結點(Descendant)：某一結點的子樹中的所有結點是這個結點的子孫

結點的層次（Level）：規定根結點在1層，其它任一結點的層數是其父結點的層數加1

樹的深度（Depth）：樹中所有結點中的最大層次是這棵樹的深度

七、樹的表示

7.1 樹的鏈表表示

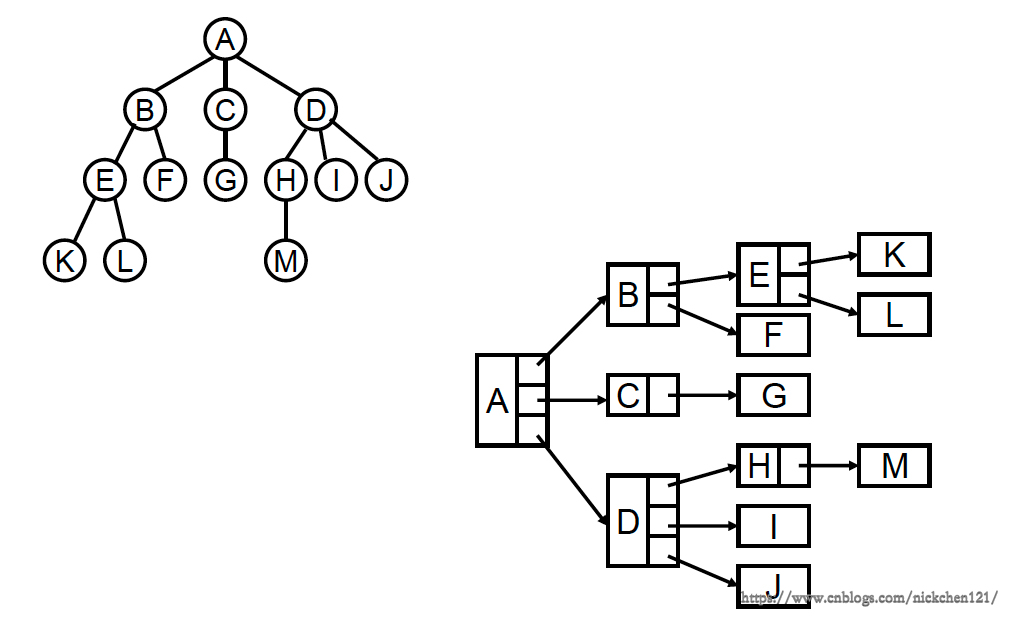
上圖所示樹的鏈表表示法有很大的缺陷，假設樹的深度非常大，并且不能保證所有樹的子結點都有3個，那么會造成很大程度的浪費。

7.2 樹的鏈表（兒子-兄弟）表示法

為了解決樹的普通鏈表表示會有空間的浪費的缺陷，我們可以把鏈表的指針設置兩個鏈接，一個鏈接指向兒子結點，另一個鏈接指向兄弟結點，如下圖所示：

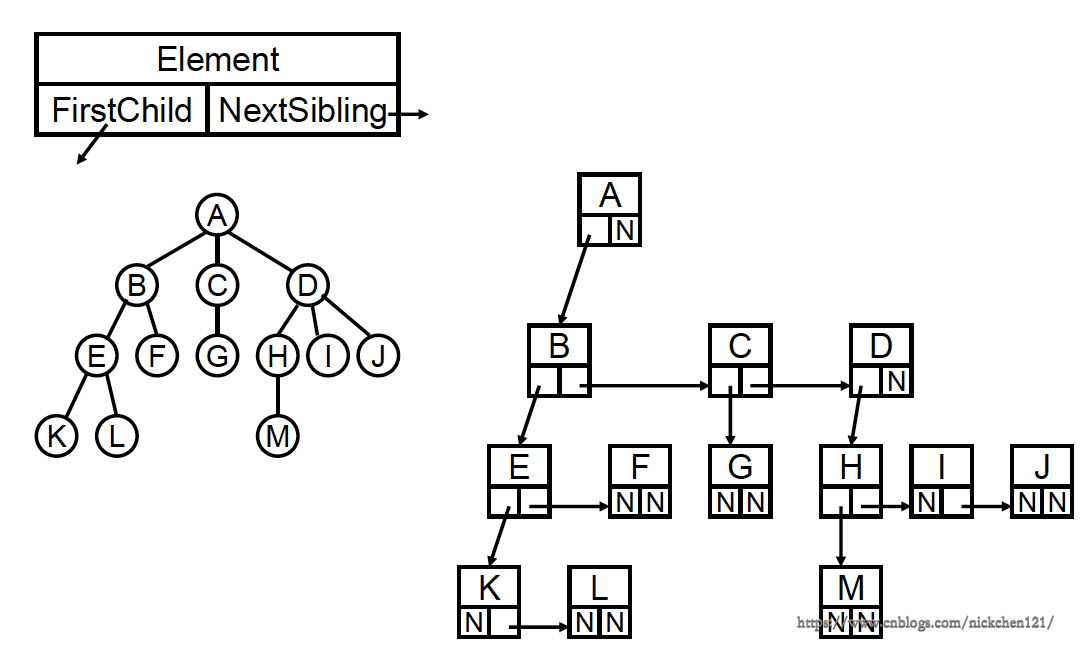
上圖所示的樹的表示方法，已經足夠完美了，但是如果我們把鏈表表示的樹旋轉45°角，會發現如下圖所示：

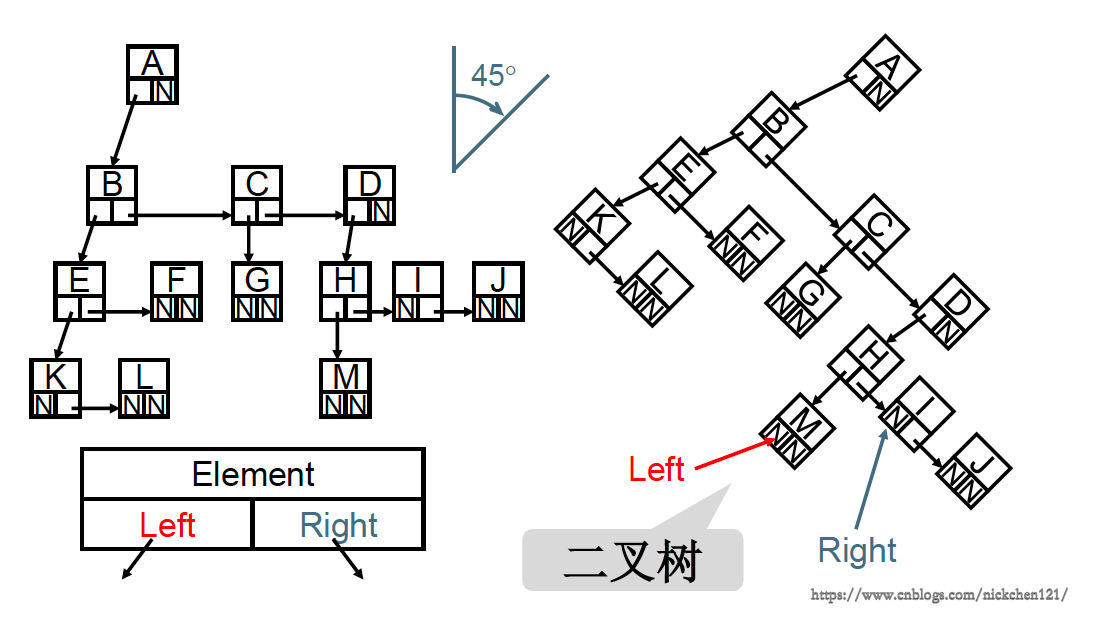
經過45°角的旋轉，我們會發現一顆二叉樹（一個結點至多擁有2個子結點的樹），也就是說最普通的樹其實可以通過二叉樹表示，也就是說我們只要把二叉樹研究透了，我們即研究透了樹。

感謝各位的閱讀！關于“python中樹是什么”這篇文章就分享到這里了，希望以上內容可以對大家有一定的幫助，讓大家可以學到更多知識，如果覺得文章不錯，可以把它分享出去讓更多的人看到吧！