Python如何通過TensorFLow進行線性模型訓練原理

這篇文章主要介紹了Python如何通過TensorFLow進行線性模型訓練原理，具有一定借鑒價值，感興趣的朋友可以參考下，希望大家閱讀完這篇文章之后大有收獲，下面讓小編帶著大家一起了解一下。

1、相關概念

例如要從一個線性分布的途中抽象出其y=kx+b的分布規律

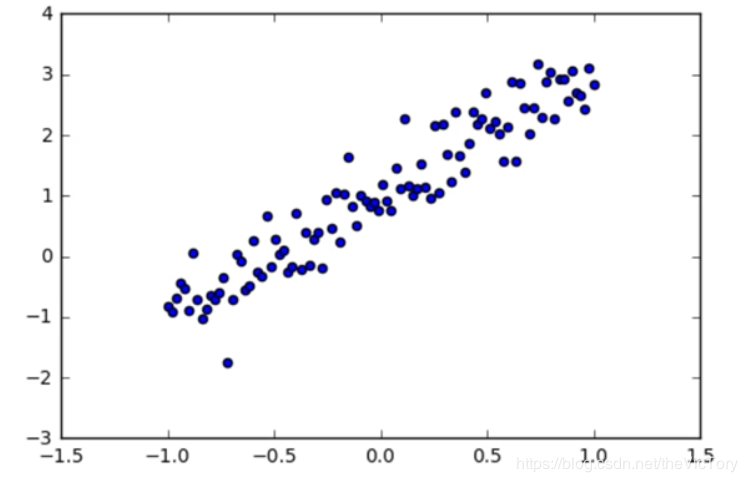
特征是輸入變量，即簡單線性回歸中的 x 變量。簡單的機器學習項目可能會使用單個特征，而比較復雜的機器學習項目可能會使用數百萬個特征。

標簽是我們要預測的事物，即簡單線性回歸中的 y 變量。

樣本是指具體的數據實例。有標簽樣本是指具有{特征,標簽}的數據，用于訓練模型，總結規律。無標簽樣本只具有特征的數據x，通過模型預測其y值。

模型是由特征向標簽映射的工具，通過機器學習建立。

訓練是指模型通過有標簽樣本來學習，確定其參數的理想值。通俗理解就是在給出一些樣本點(x,y)，總結其規律確定模型y=kx+b中的兩個參數k、b，進而利用這個方程，在只給出x的情況下計算出對應的y值。

損失是一個數值，用于表示對于單個樣本而言模型預測的準確程度。預測值與準確值相差越大，損失越大。檢查樣本并最大限度地減少模型損失的過程叫做經驗風險最小化。L1損失是標簽預測值與實際值差的絕對值。平方損失是樣本預測值與實際值的方差。

模型的訓練是一個迭代的過程，首先對模型的參數進行初始參數，得到一個初步模型并計算出特征對應的標簽值，然后經過比對計算出損失。之后對模型的參數進行調整，之后再進行預測、計算損失，如此循環直到總損失不再變化或變化很緩慢為止，這時稱該模型已經收斂。

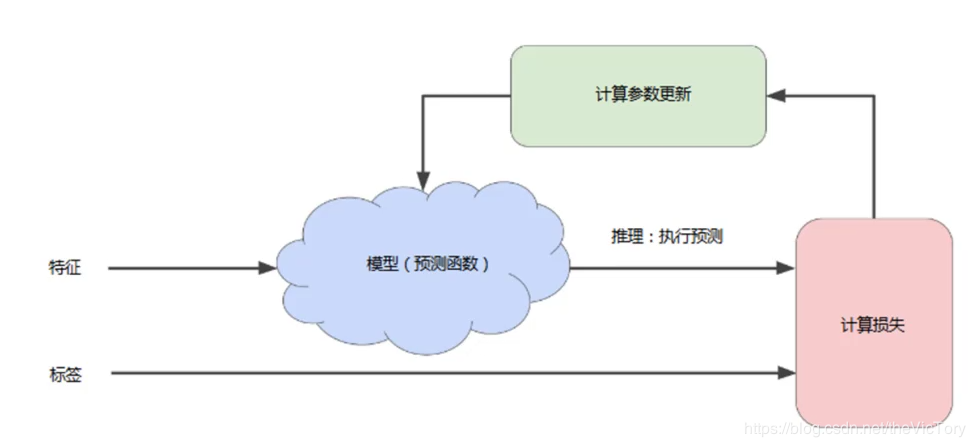
類似于對于一個二次函數，通過不斷調整x的值，找到其函數的極值點，在該點處函數的變化率為0。那么如何找到極值點，可以采用梯度下降法，即對于函數曲線，朝著其梯度值減少的方向（負梯度）探索便可以最快找到極值點。

前向傳播：根據輸入計算輸出值。反向傳播：根據優化器算法計算內部變量的調整幅度，從輸出層級開始，并往回計算每個層級，直到抵達輸入層。

在梯度下降法中，批量是指單次迭代中用于計算梯度的樣本數。隨機梯度下降法是指每次隨機選擇一個樣本進行梯度計算。

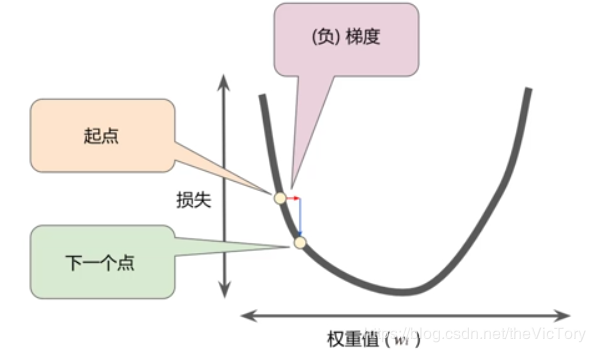
那么朝探索的方向前進多少比較合適？這就涉及到學習速率，用梯度乘以學習速率就得到了下一個點的位置，也叫做步長，如果步長過小，那么可能需要許多次才可到達目標點，如果步長過大，則可能越過目標點。

這種參數需要人為在學習之前設置參數，而不是通過訓練得到的參數，這種參數叫做超參數。超參數是編程人員用于對機器學習進行調整的旋鈕。

2、算法設計與訓練

通過Tensor FLow進行訓練的步驟主要有：準備數據、構建模型、訓練模型、進行預測

準備數據

使用的數據可以是從生活中的數據經過加工而來，也可以是人工生成的數據集，例如產生y=2x+1附近的隨機數點：

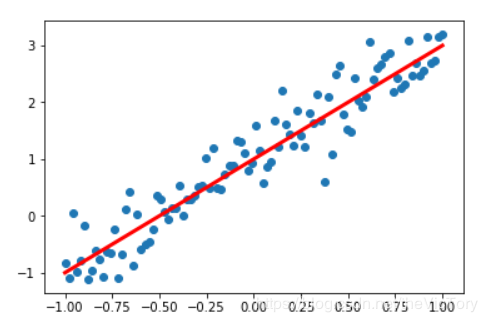
#在jupyter中設置圖像的顯示方式inline，否則圖像不顯示
%matplotlib inline         
import tensorflow as tf
import numpy as np             #Python的一種開源的數值計算擴展
import matplotlib.pyplot as plt      #Python的一種繪圖庫
 
np.random.seed(5)             #設置產生偽隨機數的類型
x=np.linspace(-1,1,100)          #在-1到1之間產生100個等差數列作為圖像的橫坐標
#根據y=2*x+1+噪聲產生縱坐標
#randn(100)表示從100個樣本的標準正態分布中返回一個樣本值，0.4為數據抖動幅度
y=2*x+1.0+np.random.randn(100)*0.4
 
plt.scatter(x,y)              #生成散點圖
plt.plot(x,2*x+1,color='red',linewidth=3)  #生成直線y=2x+1

在jupyter中繪制出了人工數據的散點圖與曲線如下：

構建模型

#定義函數模型，y=kx+b
def model(x,k,b):
  return tf.multiply(k,x)+b
#定義模型中的參數變量，并為其賦初值
k=tf.Variable(1.0,name='k')
b=tf.Variable(0,name='b')
 
#定義訓練數據的占位符，x為特征值，y為標簽
x=tf.placeholder(name='x')
y=tf.placeholder(name='y')
#通過模型得出特征值x對應的預測值yp
yp=model(x,k,b)

k、b的初始值并不會影響最終結果的得到，所以可以隨意指定一個值。

訓練模型

#訓練模型，設置訓練參數(迭代次數、學習率)
train_epoch=10
rate=0.05
#定義均方差為損失函數
loss=tf.reduce_mean(tf.square(y-yp))
#定義梯度下降優化器，并傳入參數學習率和損失函數
optimizer=tf.train.GradientDescentOptimizer(rate).minimize(loss)
 
ss=tf.Session()
init=tf.global_variables_initializer()
ss.run(init)
 
#進行多輪迭代訓練，每輪將樣本值逐個輸入模型，進行梯度下降優化操作得出參數，繪制模型曲線
for _ in range(train_epoch):
  for x1,y1 in zip(sx,sy):
    ss.run([optimizer,loss],feed_dict={x:x1,y:y1})
  tmp_k=k.eval(session=ss)
  tmp_b=b.eval(session=ss)
  plt.plot(sx,tmp_k*sx+tmp_b)
 
ss.close()

迭代次數是人為規定模型要訓練的次數。學習率不能太大或太小，根據經驗一般設置在0.01到0.1之間

采用均方差為損失函數，square求出y-yp的平方，再通過reduce_mean()求出平均值

再將之前人工生成的數據輸入到占位符時，通過zip()函數先將每個sx，sy對應壓縮為一個二維數組，然后對100個二維數組進行遍歷取出并分別填充到占位符x、y，使會話運行優化器optimizer進行迭代訓練。

可以看到運行結果如下，預測的曲線慢慢向分布的散點進行擬合

進行預測

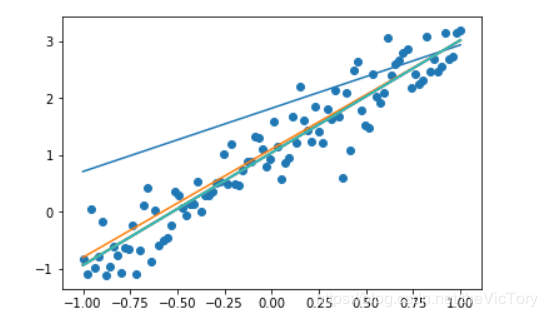
根據函數模型，y=kx+b，將得到的參數k、b和特質值x帶入即可得到標簽y的預測值

3、數組操作

Numpy是一個支持大量的維度數組與矩陣運算的python庫，通過它可以很便捷地將數據轉換為數組并進行操作。np類型的shape屬性可以輸出數組的維數構成。可以通過np.T對數組進行轉置，或者np.rashape(3,2)將數組轉換為目標形狀。例子如下

scalar=1
scalar_np=np.array(scalar)       #將標量轉化為np的數組類型
print(scalar_np.shape)         #只有np才有shape屬性，標量對應的shape輸出為()
 
#二維以上的有序數組才可以看作矩陣
matrix=[[1,2,3],[4,5,6]]
matrix_np=np.array(matrix)       #將list轉化為np矩陣
print('二維數組：',matrix)       #輸出為單行數組
print('矩陣形式：\n',matrix_np)     #結果將以多行矩陣的形式輸出
print('矩陣轉置：\n',matrix_np.T)
print('shape值',matrix_np.shape)

矩陣可以直接進行+、-、*運算，但前提是兩個矩陣的形狀相同。矩陣還可以進行叉乘運算，要求前者的行與后者的列相同，例子如下，運行結果為右上圖：

 ma=np.array([[1,2,3],[4,5,6]])
mb=np.array([[1,2],[3,4],[5,6]])
print(ma+ma)
print(ma*ma)             #矩陣點乘
print(np.matmul(ma,mb))       #矩陣叉乘

4、多元線性回歸模型

多元線性回歸模型就是在一元線性函數y=kx+b的基礎上，對于不同的特質值x1，x2...xn，將參數k擴展為多個，即y=k1x1+k2x2+...knxn+b，進而求解n+1個參數的過程。其中n個k與x相乘可以看作是兩個矩陣相乘。例如下面是一個房價預測的簡單模型，有x1~x12共12個影響房價的特質值，對應的標簽為房價，通過多元線性模型求解對應的參數k1~k12、b，從而對房價進行預測：

%matplotlib notebook
 
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.utils import shuffle
 
#利用pandas讀取數據csv文件
data=pd.read_csv('D:/Temp/data/boston.csv',header=0)
#顯示數據摘要描述信息
#print(data.describe())
data=np.array(data.values)                #將data的值轉換為np數組
for i in range(12):                    #將所有數據進行歸一化處理
  data[:,i]=data[:,i]/(data[:,i].max()-data[:,i].min())
x_data=data[:,:12]                  #截取所有行，0到11列作為特質值x
y_data=data[:,12]                   #截取所有行，第12列作為標簽值y
 
x=tf.placeholder(tf.float32,[None,12],name='x')  
#None代表行數不確定，12代表一行特征值有12個子數據
y=tf.placeholder(tf.float32,[None,1],name='y')
 
with tf.name_scope('Model'):             #定義命名空間
  k=tf.Variable(tf.random_normal([12,1],stddev=0.01),name='k')
  b=tf.Variable(1.0,name='b')
  
  def model(x,k,b):
    return tf.matmul(k,x)+b            #數組k，x進行叉乘運算再加上b
  
  yp=model(x,k,b)
 
#定義超參數：訓練次數、學習率、損失函數
train_epochs=50
learning_rate=0.01
with tf.name_scope('Loss'):
  loss_function=tf.reduce_mean(tf.square(y-yp))
#使用梯度下降法定義優化器  
optimizer=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)
 
ss=tf.Session()
init=tf.global_variables_initializer()
ss.run(init)
loss_list=[]
 
for _ in range(train_epochs):
  loss_sum=0
  for(xs,ys)in zip(x_data,y_data):
    xs=xs.reshape(1,12)             #調整數據的維數格式以匹配占位符x
    ys=ys.reshape(1,1)
    _,loss=ss.run([optimizer,loss_function],feed_dict={x:xs,y:ys})
    loss_sum+=loss
    
  shuffle(x_data,y_data)              #每輪循環后，打亂數據順序
  k_tmp=k.eval(session=ss)
  b_tmp=b.eval(session=ss)
  print('k:',k_tmp,',b:',b_tmp)
  
  loss_avg=loss_sum/len(y_data)            #求每輪的損失值
  loss_list.append(loss_avg)  
  
plt.plot(loss_list)

注：

pandas是一個python庫，可以提供高性能且易使用的數據結構與數據分析工具，可以從csv、excel、txt、sql等文件中讀取數據，并且將數據結構自動轉換為Numpy多維數組。

在使用梯度下降法進行多元線性回歸模型訓練時，如果不同的特征值取值范圍相差過大（比如有的特質值取值為0.3~0.7，有點特質值在300~700），就會影響訓練結果的得出。因此需要對數據進行歸一化處理，即用特征值/(最大值-最小值)，也就是通過放縮將數據都統一到0~1之間。

通過tf.name_scope()定義命名空間，定義的變量名只在當前空間內有效，防止命名沖突。

在初始化變量k時，通過tf.random_normal()從正太分布[1,12]之間隨機選取一個值，其方差stddev=0.01

由于在定義占位符時x為[None,12]類型的二維數組，所以在填充數據時需要通過xs.reshape(1,12)將數據xs重新排列為一維含有12個元素，二維含有1個子數組的二維數組，同理，y也需要轉換。

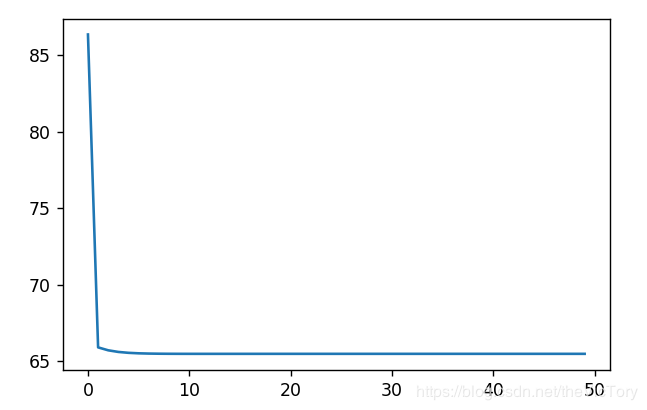
實現定義loss_list用于保存損失值，在每輪訓練后求出損失值的平均值保存到loss_list，最后將其打印成一幅圖，可以看到損失值從一開始急速下降，直到最后變化趨于平緩。

運行結果如下，截取部分的參數值以及損失值的曲線：

感謝你能夠認真閱讀完這篇文章，希望小編分享的“Python如何通過TensorFLow進行線性模型訓練原理”這篇文章對大家有幫助，同時也希望大家多多支持億速云，關注億速云行業資訊頻道，更多相關知識等著你來學習!