您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
Python中支持Convex Optimization(凸規劃)的模塊為CVXOPT,其安裝方式為:
pip install cvxopt
一、數學基礎
二次型
二次型(quadratic form):n個變量的二次多項式稱為二次型,即在一個多項式中,未知數的個數為任意多個,但每一項的次數都為2的多項式。其基本形式如下
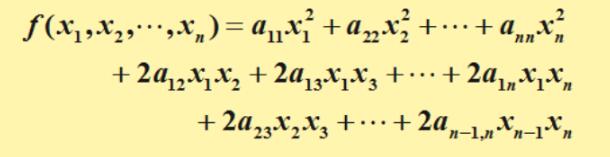
亦可寫作,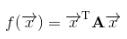 ,稱作二次型的矩陣表示,其中A是對稱矩陣。仿照如下的定義,我們可以直接在其基本形式和矩陣表示之間相互轉化。
,稱作二次型的矩陣表示,其中A是對稱矩陣。仿照如下的定義,我們可以直接在其基本形式和矩陣表示之間相互轉化。
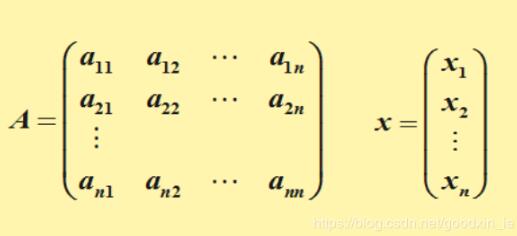
2.正定矩陣
設A是n階實對稱矩陣, 如果對任意一非零實向量X,都使二次型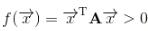 成立,則稱f(X)為正定二次型,矩陣A稱為正定矩陣(Positive Definite),A為正定矩陣。
成立,則稱f(X)為正定二次型,矩陣A稱為正定矩陣(Positive Definite),A為正定矩陣。
相應的,如果對任意一非零實向量X,都使二次型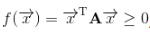 成立,則稱f(X)為半正定二次型,A為半正定矩陣。
成立,則稱f(X)為半正定二次型,A為半正定矩陣。
3.二次規劃問題
二次規劃是指,帶有二次型目標函數和約束條件的最優化問題。其標準形式如下:
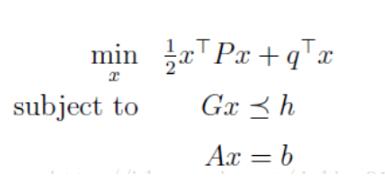
即在Gx<h 和Ax=b的約束下,最小化目標函數。其中,當P是正定矩陣時,目標函數存在全局唯一最優解;P是半正定矩陣時,目標函數是凸函數,存在全局最優解(不唯一);P是不定矩陣時,目標函數非凸,存在多個局部最小值和穩定點,為np難問題。(本篇博客中我們不考慮非正定情況)。
二、python程序求解
工具包:Cvxopt python 凸優化包
函數原型:Cvxopt.solvers.qp(P,q,G,h,A,b)
P,q,G,h,A,b的含義參見上面的二次規劃問題標準形式。
編程求解思路:
1.對于一個給定的二次規劃問題,先轉換為標準形式(參見數學基礎中所講的二次型二中形式轉換)
2.對照標準形勢,構建出矩陣P,q,G,h,A,b
3.調用result=Cvxopt.solvers.qp(P,q,G,h,A,b)求解
4.print(result)查看結果,其中result是一個字典,我們可直接獲得其某個屬性,e.g. print(result['x'])
下面我們來看一個例子
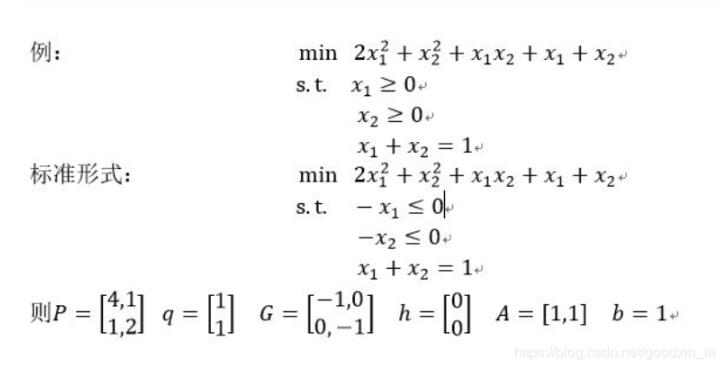
import pprint
from cvxopt import matrix, solvers
P = matrix([[4.0,1.0],[1.0,2.0]])
q = matrix([1.0,1.0])
G = matrix([[-1.0,0.0],[0.0,-1.0]])
h = matrix([0.0,0.0])
A = matrix([1.0,1.0],(1,2))#原型為cvxopt.matrix(array,dims),等價于A = matrix([[1.0],[1.0]])
b = matrix([1.0])
result = solvers.qp(P,q,G,h,A,b)
print('x\n',result['x'])
運行結果:
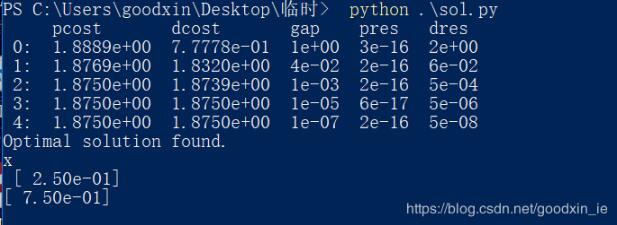
注意事項:
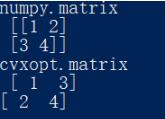
cvxopt.matrix與numpy.matrix的排列順序不同,其中cvxopt.matrix是列優先,numpy.matrix是行優先。具體可見下面實例
import numpy as np
from cvxopt import matrix
a = np.matrix([[1,2],[3,4]])
b = matrix([[1,2],[3,4]])
print('numpy.matrix',a)
print('cvxopt.matrix',b)
運行結果:
以上這篇使用python求解二次規劃的問題就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。