怎么用Python進行時間序列預測

這篇文章主要介紹怎么用Python進行時間序列預測，文中介紹的非常詳細，具有一定的參考價值，感興趣的小伙伴們一定要看完！

python的數據類型有哪些?

python的數據類型：1. 數字類型，包括int（整型）、long（長整型）和float（浮點型）。2.字符串，分別是str類型和unicode類型。3.布爾型，Python布爾類型也是用于邏輯運算，有兩個值：True（真）和False（假）。4.列表，列表是Python中使用最頻繁的數據類型，集合中可以放任何數據類型。5. 元組，元組用”()”標識，內部元素用逗號隔開。6. 字典，字典是一種鍵值對的集合。7. 集合，集合是一個無序的、不重復的數據組合。

數據準備

數據集（JetRail高鐵的乘客數量）下載.

假設要解決一個時序問題：根據過往兩年的數據（2012 年 8 月至 2014 年 8月），需要用這些數據預測接下來 7 個月的乘客數量。

import pandas as pd 
import numpy as np 
import matplotlib.pyplot as plt
 
df = pd.read_csv('train.csv')
df.head()
df.shape

依照上面的代碼，我們獲得了 2012-2014 年兩年每個小時的乘客數量。為了解釋每種方法的不同之處，以每天為單位構造和聚合了一個數據集。

• 從 2012 年 8 月- 2013 年 12 月的數據中構造一個數據集。

• 創建 train and test 文件用于建模。前 14 個月（ 2012 年 8 月- 2013 年 10 月）用作訓練數據，后兩個月（2013 年 11 月 – 2013 年 12 月）用作測試數據。

• 以每天為單位聚合數據集。

import pandas as pd
import matplotlib.pyplot as plt
 
# Subsetting the dataset
# Index 11856 marks the end of year 2013
df = pd.read_csv('train.csv', nrows=11856)
 
# Creating train and test set
# Index 10392 marks the end of October 2013
train = df[0:10392]
test = df[10392:]
 
# Aggregating the dataset at daily level
df['Timestamp'] = pd.to_datetime(df['Datetime'], format='%d-%m-%Y %H:%M') # 4位年用Y，2位年用y
df.index = df['Timestamp']
df = df.resample('D').mean() #按天采樣，計算均值
 
train['Timestamp'] = pd.to_datetime(train['Datetime'], format='%d-%m-%Y %H:%M')
train.index = train['Timestamp']
train = train.resample('D').mean() #
 
test['Timestamp'] = pd.to_datetime(test['Datetime'], format='%d-%m-%Y %H:%M')
test.index = test['Timestamp']
test = test.resample('D').mean()
 
#Plotting data
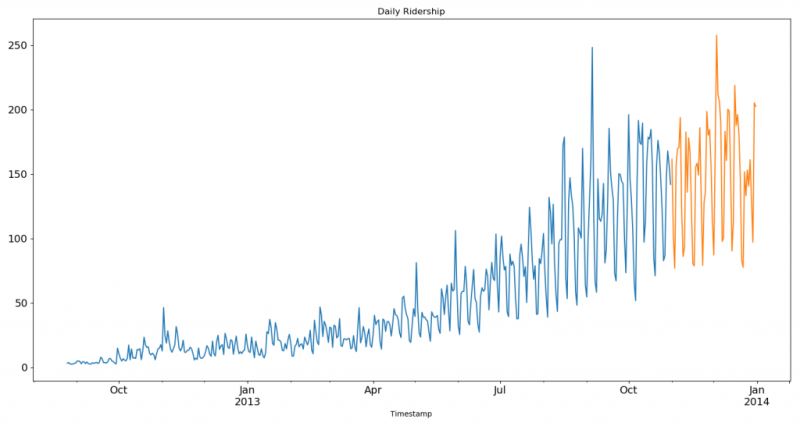
train.Count.plot(figsize=(15,8), title= 'Daily Ridership', fontsize=14)
test.Count.plot(figsize=(15,8), title= 'Daily Ridership', fontsize=14)
plt.show()

我們將數據可視化（訓練數據和測試數據一起），從而得知在一段時間內數據是如何變化的。

方法1：樸素法

假設 y 軸表示物品的價格，x 軸表示時間（天）

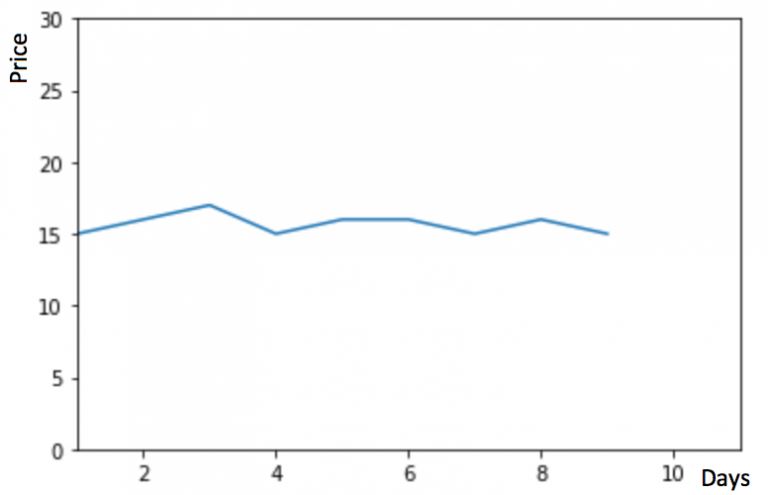
如果數據集在一段時間內都很穩定，我們想預測第二天的價格，可以取前面一天的價格，預測第二天的值。這種假設第一個預測點和上一個觀察點相等的預測方法就叫樸素法。即 $\hat{y_{t+1}} = y_t$

dd = np.asarray(train['Count'])
y_hat = test.copy()
y_hat['naive'] = dd[len(dd) - 1]
plt.figure(figsize=(12, 8))
plt.plot(train.index, train['Count'], label='Train')
plt.plot(test.index, test['Count'], label='Test')
plt.plot(y_hat.index, y_hat['naive'], label='Naive Forecast')
plt.legend(loc='best')
plt.title("Naive Forecast")
plt.show()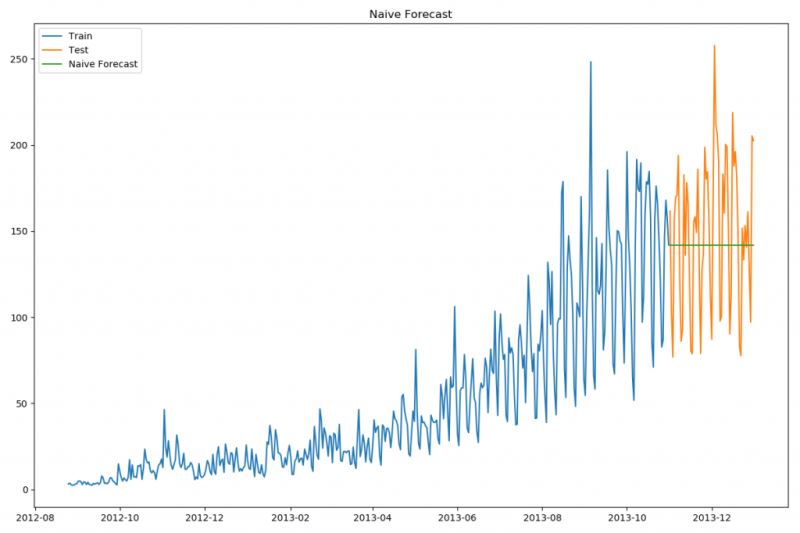

樸素法并不適合變化很大的數據集，最適合穩定性很高的數據集。我們計算下均方根誤差，檢查模型在測試數據集上的準確率：

from sklearn.metrics import mean_squared_error
from math import sqrt
 
rms = sqrt(mean_squared_error(test['Count'], y_hat['naive']))
print(rms)

最終均方誤差RMS為：43.91640614391676

方法2：簡單平均法

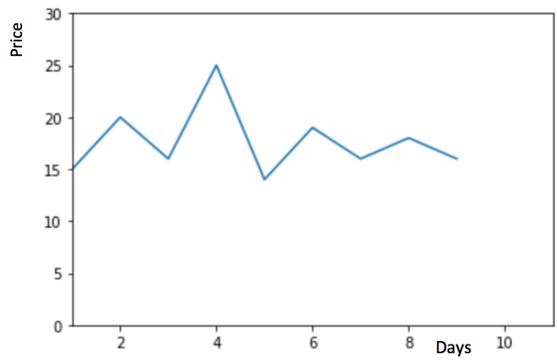
物品價格會隨機上漲和下跌，平均價格會保持一致。我們經常會遇到一些數據集，雖然在一定時期內出現小幅變動，但每個時間段的平均值確實保持不變。這種情況下，我們可以預測出第二天的價格大致和過去天數的價格平均值一致。這種將預期值等同于之前所有觀測點的平均值的預測方法就叫簡單平均法。即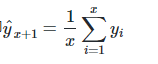

y_hat_avg = test.copy()
y_hat_avg['avg_forecast'] = train['Count'].mean()
plt.figure(figsize=(12,8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['avg_forecast'], label='Average Forecast')
plt.legend(loc='best')
plt.show()

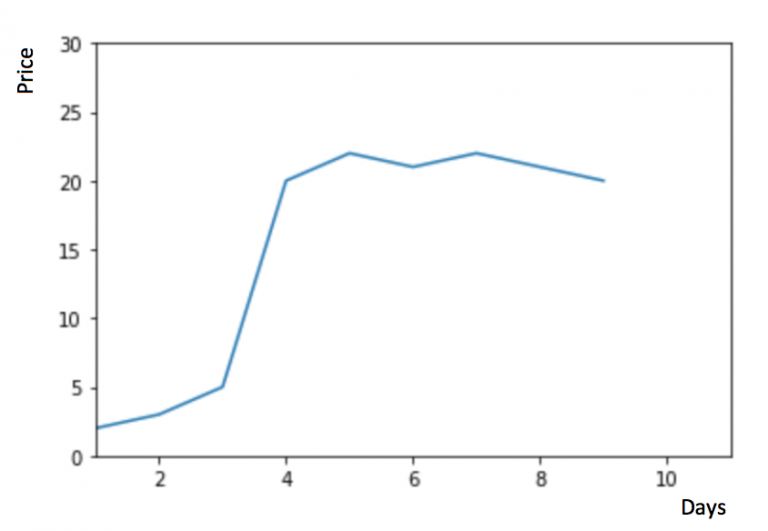
物品價格在一段時間內大幅上漲，但后來又趨于平穩。我們也經常會遇到這種數據集，比如價格或銷售額某段時間大幅上升或下降。如果我們這時用之前的簡單平均法，就得使用所有先前數據的平均值，但在這里使用之前的所有數據是說不通的，因為用開始階段的價格值會大幅影響接下來日期的預測值。因此，我們只取最近幾個時期的價格平均值。很明顯這里的邏輯是只有最近的值最要緊。這種用某些窗口期計算平均值的預測方法就叫移動平均法。

計算移動平均值涉及到一個有時被稱為“滑動窗口”的大小值p。使用簡單的移動平均模型，我們可以根據之前數值的固定有限數p的平均值預測某個時序中的下一個值。這樣，對于所有的 i > p：

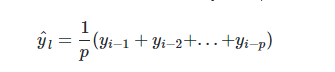
在上文移動平均法可以看到，我們對“p”中的觀察值賦予了同樣的權重。但是我們可能遇到一些情況，比如“p”中每個觀察值會以不同的方式影響預測結果。將過去觀察值賦予不同權重的方法就叫做加權移動平均法。加權移動平均法其實還是一種移動平均法，只是“滑動窗口期”內的值被賦予不同的權重，通常來講，最近時間點的值發揮的作用更大了。即

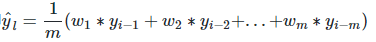
這種方法并非選擇一個窗口期的值，而是需要一列權重值（相加后為1）。例如，如果我們選擇[0.40, 0.25, 0.20, 0.15]作為權值，我們會為最近的4個時間點分別賦給40%，25%，20%和15%的權重。

方法4：簡單指數法

我們注意到簡單平均法和加權移動平均法在選取時間點的思路上存在較大的差異。我們就需要在這兩種方法之間取一個折中的方法，在將所有數據考慮在內的同時也能給數據賦予不同非權重。例如，相比更早時期內的觀測值，它會給近期的觀測值賦予更大的權重。按照這種原則工作的方法就叫做簡單指數平滑法。它通過加權平均值計算出預測值，其中權重隨著觀測值從早期到晚期的變化呈指數級下降，最小的權重和最早的觀測值相關：

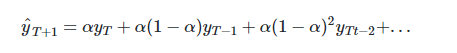
其中0≤α≤1是平滑參數。對時間點T+1的單步預測值是時序$y_1,…,y_T$的所有觀測值的加權平均數。權重下降的速率由參數α控制，預測值$\hat{y}_x$是$\alpha \cdot y_t $與$(1-\alpha) \cdot \hat{y}_x$的和。

因此，它可以寫為：

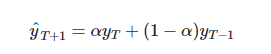
所以本質上，我們是用兩個權重α和1?α得到一個加權移動平均值，讓表達式呈遞進形式。

from statsmodels.tsa.api import SimpleExpSmoothing
 
y_hat_avg = test.copy()
fit = SimpleExpSmoothing(np.asarray(train['Count'])).fit(smoothing_level=0.6, optimized=False)
y_hat_avg['SES'] = fit.forecast(len(test))
plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['SES'], label='SES')
plt.legend(loc='best')
plt.show()

模型中使用的α值為0.6，我們可以用測試集繼續調整參數以生成一個更好的模型。

方法5：霍爾特(Holt)線性趨勢法

假設y軸表示某個物品的價格，x軸表示時間（天）。

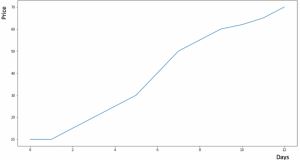
如果物品的價格是不斷上漲的（見上圖），我們上面的方法并沒有考慮這種趨勢，即我們在一段時間內觀察到的價格的總體模式。

每個時序數據集可以分解為相應的幾個部分：趨勢（Trend），季節性(Seasonal)和殘差(Residual)。任何呈現某種趨勢的數據集都可以用霍爾特線性趨勢法用于預測。

import statsmodels.api as sm
 
sm.tsa.seasonal_decompose(train['Count']).plot()
result = sm.tsa.stattools.adfuller(train['Count'])
plt.show()

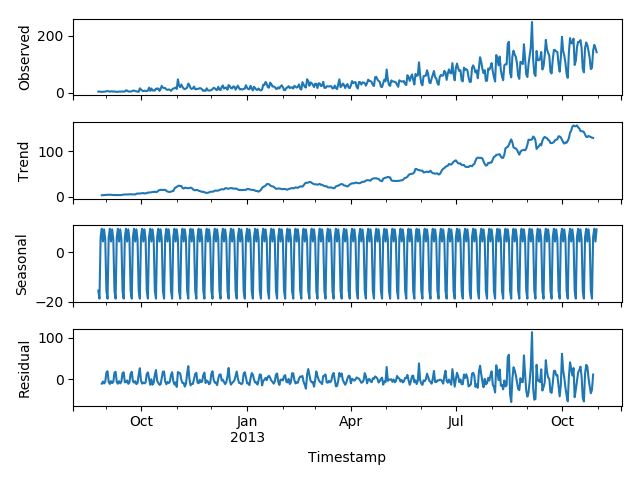
我們從圖中可以看出，該數據集呈上升趨勢。因此我們可以用霍爾特線性趨勢法預測未來價格。該算法包含三個方程：一個水平方程，一個趨勢方程，一個方程將二者相加以得到預測值$\hat{y}$：

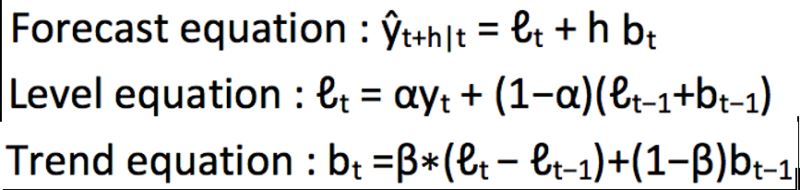
我們在上面算法中預測的值稱為水平（level）。正如簡單指數平滑一樣，這里的水平方程顯示它是觀測值和樣本內單步預測值的加權平均數，趨勢方程顯示它是根據 ?(t)??(t?1) 和之前的預測趨勢 b(t?1) 在時間t處的預測趨勢的加權平均值。

我們將這兩個方程相加，得出一個預測函數。我們也可以將兩者相乘而不是相加得到一個乘法預測方程。當趨勢呈線性增加和下降時，我們用相加得到的方程；當趨勢呈指數級增加或下降時，我們用相乘得到的方程。實踐操作顯示，用相乘得到的方程，預測結果會更穩定，但用相加得到的方程，更容易理解。

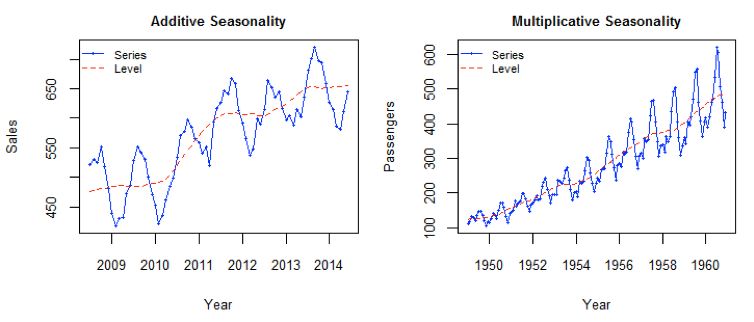
from statsmodels.tsa.api import Holt
 
y_hat_avg = test.copy()
 
fit = Holt(np.asarray(train['Count'])).fit(smoothing_level=0.3, smoothing_slope=0.1)
y_hat_avg['Holt_linear'] = fit.forecast(len(test))
 
plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['Holt_linear'], label='Holt_linear')
plt.legend(loc='best')
plt.show()

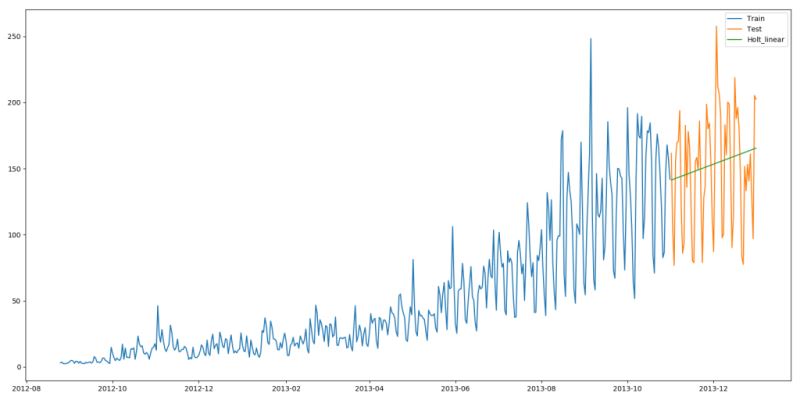
這種方法能夠準確地顯示出趨勢，因此比前面的幾種模型效果更好。如果調整一下參數，結果會更好。

方法6：Holt-Winters季節性預測模型

在應用這種算法前，我們先介紹一個新術語。假如有家酒店坐落在半山腰上，夏季的時候生意很好，顧客很多，但每年其余時間顧客很少。因此，每年夏季的收入會遠高于其它季節，而且每年都是這樣，那么這種重復現象叫做“季節性”（Seasonality）。如果數據集在一定時間段內的固定區間內呈現相似的模式，那么該數據集就具有季節性。

我們之前討論的5種模型在預測時并沒有考慮到數據集的季節性，因此我們需要一種能考慮這種因素的方法。應用到這種情況下的算法就叫做Holt-Winters季節性預測模型，它是一種三次指數平滑預測，其背后的理念就是除了水平和趨勢外，還將指數平滑應用到季節分量上。

Holt-Winters季節性預測模型由預測函數和三次平滑函數——一個是水平函數?t，一個是趨勢函數bt，一個是季節分量 st，以及平滑參數α,β和γ。

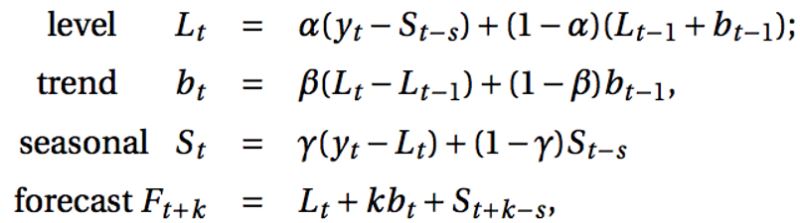
其中 s 為季節循環的長度，0≤α≤ 1, 0 ≤β≤ 1 ， 0≤γ≤ 1。水平函數為季節性調整的觀測值和時間點t處非季節預測之間的加權平均值。趨勢函數和霍爾特線性方法中的含義相同。季節函數為當前季節指數和去年同一季節的季節性指數之間的加權平均值。在本算法，我們同樣可以用相加和相乘的方法。當季節性變化大致相同時，優先選擇相加方法，而當季節變化的幅度與各時間段的水平成正比時，優先選擇相乘的方法。

from statsmodels.tsa.api import ExponentialSmoothing
 
y_hat_avg = test.copy()
fit1 = ExponentialSmoothing(np.asarray(train['Count']), seasonal_periods=7, trend='add', seasonal='add', ).fit()
y_hat_avg['Holt_Winter'] = fit1.forecast(len(test))
plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['Holt_Winter'], label='Holt_Winter')
plt.legend(loc='best')
plt.show()

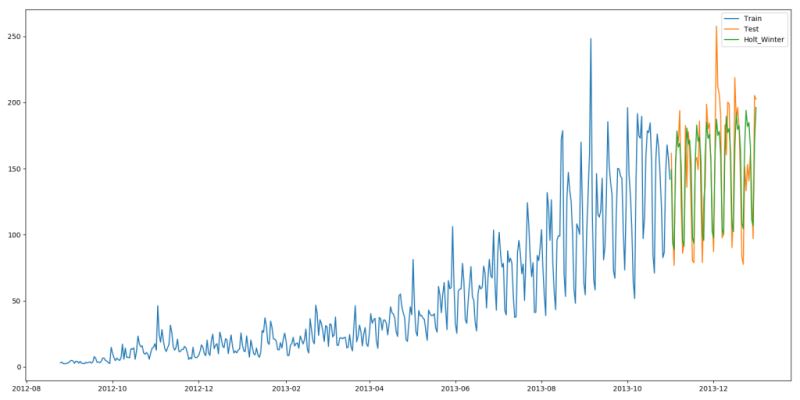
我們可以看到趨勢和季節性的預測準確度都很高。我們選擇了 seasonal_period = 7作為每周重復的數據。也可以調整其它其它參數，我在搭建這個模型的時候用的是默認參數。你可以試著調整參數來優化模型。

方法7：自回歸移動平均模型（ARIMA）

另一個場景的時序模型是自回歸移動平均模型（ARIMA）。指數平滑模型都是基于數據中的趨勢和季節性的描述，而自回歸移動平均模型的目標是描述數據中彼此之間的關系。ARIMA的一個優化版就是季節性ARIMA。它像Holt-Winters季節性預測模型一樣，也把數據集的季節性考慮在內。

import statsmodels.api as sm
 
y_hat_avg = test.copy()
fit1 = sm.tsa.statespace.SARIMAX(train.Count, order=(2, 1, 4), seasonal_order=(0, 1, 1, 7)).fit()
y_hat_avg['SARIMA'] = fit1.predict(start="2013-11-1", end="2013-12-31", dynamic=True)
plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['SARIMA'], label='SARIMA')
plt.legend(loc='best')
plt.show()

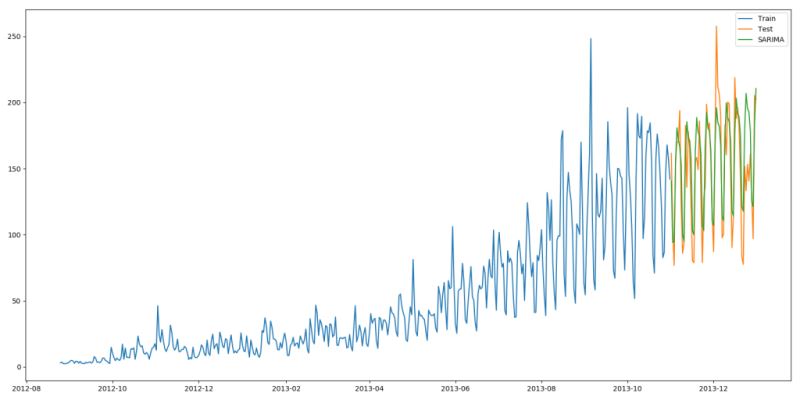
我們可以看到使用季節性 ARIMA 的效果和Holt-Winters差不多。我們根據 ACF（自相關函數）和 PACF（偏自相關） 圖選擇參數。如果你為 ARIMA 模型選擇參數時遇到了困難，可以用 R 語言中的 auto.arima。

最后，我們將這幾種模型的準確度比較一下：

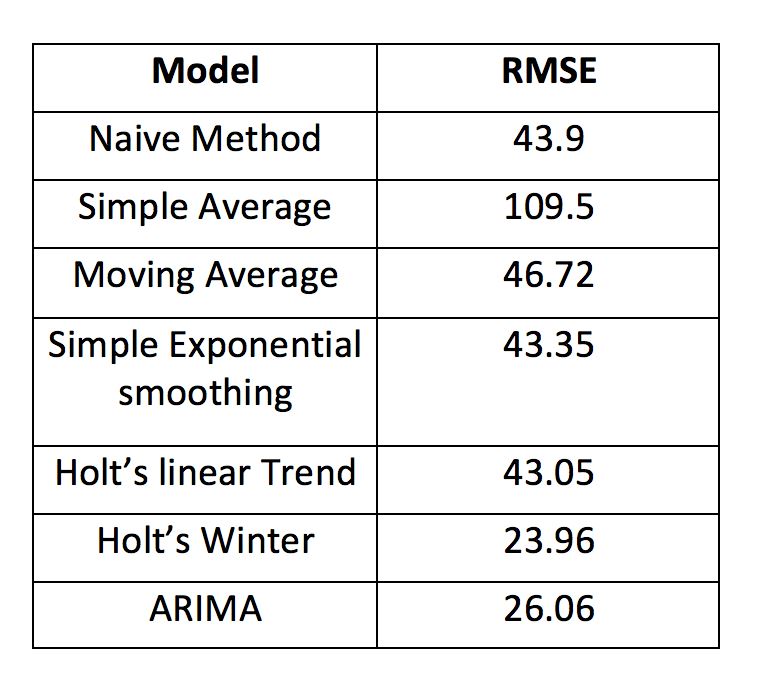
以上是“怎么用Python進行時間序列預測”這篇文章的所有內容，感謝各位的閱讀！希望分享的內容對大家有幫助，更多相關知識，歡迎關注億速云行業資訊頻道！