您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了TensorFlow tf.nn.conv2d_transpose實現反卷積的方法,內容清晰明了,對此有興趣的小伙伴可以學習一下,相信大家閱讀完之后會有幫助。
首先無論你如何理解反卷積,請時刻記住一點,反卷積操作是卷積的反向
如果你隨時都記住上面強調的重點,那你基本就理解一大半了,接下來通過一些函數的介紹為大家強化這個觀念
conv2d_transpose(value, filter, output_shape, strides, padding="SAME", data_format="NHWC", name=None)
除去name參數用以指定該操作的name,與方法有關的一共六個參數:
第一個參數value:指需要做反卷積的輸入圖像,它要求是一個Tensor
第二個參數filter:卷積核,它要求是一個Tensor,具有[filter_height, filter_width, out_channels, in_channels]這樣的shape,具體含義是[卷積核的高度,卷積核的寬度,卷積核個數,圖像通道數]
第三個參數output_shape:反卷積操作輸出的shape,細心的同學會發現卷積操作是沒有這個參數的,那這個參數在這里有什么用呢?下面會解釋這個問題
第四個參數strides:反卷積時在圖像每一維的步長,這是一個一維的向量,長度4
第五個參數padding:string類型的量,只能是"SAME","VALID"其中之一,這個值決定了不同的卷積方式
第六個參數data_format:string類型的量,'NHWC'和'NCHW'其中之一,這是tensorflow新版本中新加的參數,它說明了value參數的數據格式。'NHWC'指tensorflow標準的數據格式[batch, height, width, in_channels],'NCHW'指Theano的數據格式,[batch, in_channels,height, width],當然默認值是'NHWC'
開始之前務必了解卷積的過程,參考我的另一篇文章:https://www.jb51.net/article/177798.htm
首先定義一個單通道圖和3個卷積核
x1 = tf.constant(1.0, shape=[1,3,3,1]) kernel = tf.constant(1.0, shape=[3,3,3,1])
先別著急!我們不直接用反卷積函數,而是再定義一些圖
x2 = tf.constant(1.0, shape=[1,6,6,3]) x3 = tf.constant(1.0, shape=[1,5,5,3])
x2是6×6的3通道圖,x3是5×5的3通道圖
好了,接下來對x3做一次卷積操作
y2 = tf.nn.conv2d(x3, kernel, strides=[1,2,2,1], padding="SAME")
所以返回的y2是一個單通道的圖,如果你了解卷積過程,很容易看出來y2是[1,3,3,1]的Tensor,y2的結果如下:
[[[[ 12.] [ 18.] [ 12.]] [[ 18.] [ 27.] [ 18.]] [[ 12.] [ 18.] [ 12.]]]]
又一個很重要的部分!tf.nn.conv2d中的filter參數,是[filter_height, filter_width, in_channels, out_channels]的形式,而tf.nn.conv2d_transpose中的filter參數,是[filter_height, filter_width, out_channels,in_channels]的形式,注意in_channels和out_channels反過來了!因為兩者互為反向,所以輸入輸出要調換位置
既然y2是卷積操作的返回值,那我們當然可以對它做反卷積,反卷積操作返回的Tensor,應該和x3的shape是一樣的(不難理解,因為是卷積的反過程)
y3 = tf.nn.conv2d_transpose(y2,kernel,output_shape=[1,5,5,3], strides=[1,2,2,1],padding="SAME")
好,現在返回的y3果然是[1,5,5,3]的Tensor,結果如下:
[[[[ 12. 12. 12.] [ 30. 30. 30.] [ 18. 18. 18.] [ 30. 30. 30.] [ 12. 12. 12.]] [[ 30. 30. 30.] [ 75. 75. 75.] [ 45. 45. 45.] [ 75. 75. 75.] [ 30. 30. 30.]] [[ 18. 18. 18.] [ 45. 45. 45.] [ 27. 27. 27.] [ 45. 45. 45.] [ 18. 18. 18.]] [[ 30. 30. 30.] [ 75. 75. 75.] [ 45. 45. 45.] [ 75. 75. 75.] [ 30. 30. 30.]] [[ 12. 12. 12.] [ 30. 30. 30.] [ 18. 18. 18.] [ 30. 30. 30.] [ 12. 12. 12.]]]]
這個結果是怎么得來的?可以用一張動圖來說明,圖片來源:反卷積的真正含義
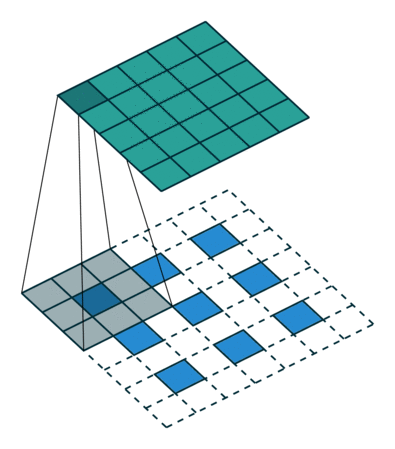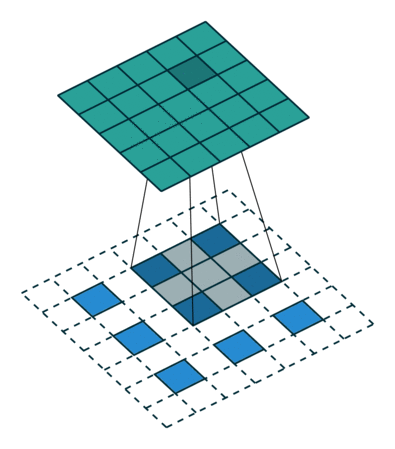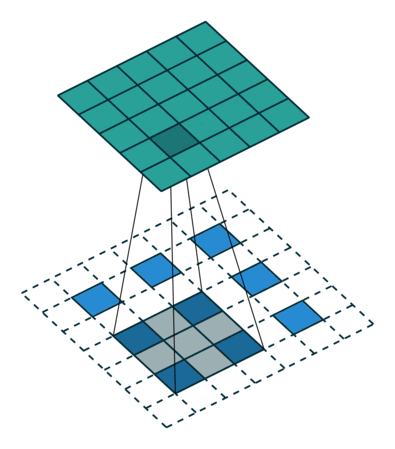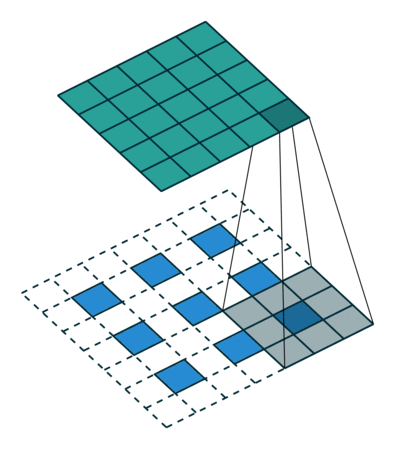
看起來,tf.nn.conv2d_transpose的output_shape似乎是多余的,因為知道了原圖,卷積核,步長顯然是可以推出輸出圖像大小的,那為什么要指定output_shape呢?
看這樣一種情況:
y4 = tf.nn.conv2d(x2, kernel, strides=[1,2,2,1], padding="SAME")
我們把上面的x2也做卷積,獲得shape為[1,3,3,1]的y4如下:
[[[[ 27.] [ 27.] [ 18.]] [[ 27.] [ 27.] [ 18.]] [[ 18.] [ 18.] [ 12.]]]]
[1,6,6,3]和[1,5,5,3]的圖經過卷積得到了相同的大小,[1,3,3,1]
讓我們再反過來看,那么[1,3,3,1]的圖反卷積后得到什么呢?產生了兩種情況。所以這里指定output_shape是有意義的,當然隨意指定output_shape是不允許的,如下情況程序會報錯:
y5 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,10,10,3],strides=[1,2,2,1],padding="SAME")
以上是stride為2的情況,為1時也類似,當卷積核大于原圖時,默認用VALID方式(用SAME就無意義了)參考下圖:
程序清單:
import tensorflow as tf x1 = tf.constant(1.0, shape=[1,3,3,1]) x2 = tf.constant(1.0, shape=[1,6,6,3]) x3 = tf.constant(1.0, shape=[1,5,5,3]) kernel = tf.constant(1.0, shape=[3,3,3,1]) y1 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,6,6,3], strides=[1,2,2,1],padding="SAME") y2 = tf.nn.conv2d(x3, kernel, strides=[1,2,2,1], padding="SAME") y3 = tf.nn.conv2d_transpose(y2,kernel,output_shape=[1,5,5,3], strides=[1,2,2,1],padding="SAME") y4 = tf.nn.conv2d(x2, kernel, strides=[1,2,2,1], padding="SAME") ''' Wrong!!This is impossible y5 = tf.nn.conv2d_transpose(x1,kernel,output_shape=[1,10,10,3],strides=[1,2,2,1],padding="SAME") ''' sess = tf.Session() tf.global_variables_initializer().run(session=sess) x1_decov, x3_cov, y2_decov, x2_cov=sess.run([y1,y2,y3,y4]) print(x1_decov.shape) print(x3_cov.shape) print(y2_decov.shape) print(x2_cov.shape)
看完上述內容,是不是對TensorFlow tf.nn.conv2d_transpose實現反卷積的方法有進一步的了解,如果還想學習更多內容,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。