您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
問題1:半徑為5000米環狀空間站,為使其產生相當于地球1g的重力加速度,求空間站的轉轉周期是多少?
為解決這個問題,我們先來復習一下牛頓三大運動定律:
牛頓第一運動定律:
一個物體在沒有受到外力作用下,保持勻速直線運動不變。
牛頓第二運動定律:
物體做加速運動時所需要的力F與物體質量m成正比、與其加速度a成正比。表達式為:
F=ma?
單位: F 牛頓、m千克、a 米/秒2
牛頓第三運動定律:
作用于物體的作用力與反作用力大小相等,方向相反,且在一條直線上。
做圓周運動的向心加速度a為:
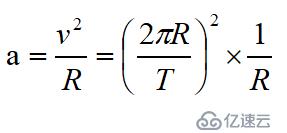
(圓周運動的線速度V等于圓的周長除以周期T)
所以做圓周運動的向心加速度a化簡為:
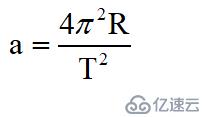
根據牛頓第三運動定律:
物體受到的離心力=飛船旋轉所產生的向心力,就是:
ma1=ma2
其中a1就是我們希望的地球重力加速度g
a2是飛船旋轉做運動所產生的向心力
所以:
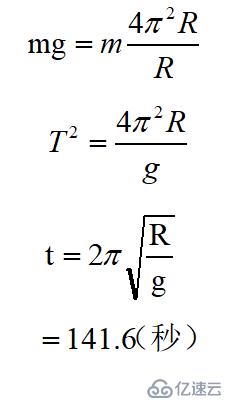
其中:
R為飛船半徑5000米
g為地球重力加速度,為9.8米/秒2
線速度V可以通過公式V=2πR/T 求得。
問題2:空間站模擬重力加速度1g,自轉一周24小時,求空間站半徑:
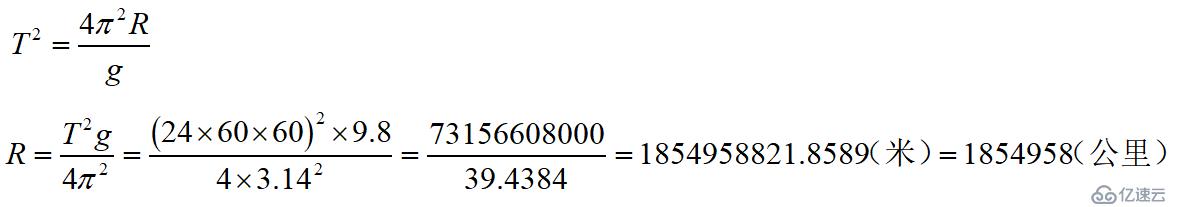
與之對比,太陽的半徑為696300公里。
好家伙,該空間站半徑是太陽半徑的2倍多。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。